Иллюстрированный самоучитель по Mathematica 5

За гранью простого. Новый вид науки.

При дальнейшем увеличении г поведение последовательности {хn} опять изменяется. Возникает цикл S⁴: х_4n › а₁, x_4n+1 › a₂, х_4n+1 › a₃ > x_4n+3 › а₄ при n › ∞, причем а2 = f(a1), а3=f(a2), аn =f(an). Численность популяции начинает колебаться с периодом в 4 года.

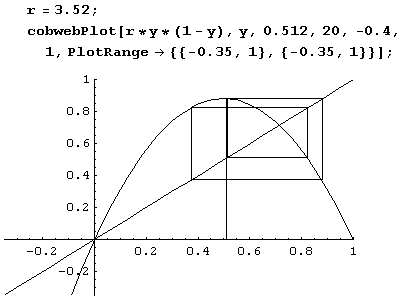
Но и это еще не все. Приведем еще несколько примеров поведения наших последовательностей.

Последовательно увеличивая значение параметра, мы увидим циклы S⁸, S¹⁶, S³² и т.д. При этом каждый раз цикл S² теряет устойчивость, и устойчивым становится цикл S². Наконец, при некотором значении г (его иногда обозначают г") формула x_n+1 = rхn(1-хn) дает уже непериодическую последовательность {xn}.

Полученная нами картина оказалась очень интересной. Во-первых, в поразительно простой модели х_n+1 = rхn(1-хn) заложено очень сложное поведение. Во-вторых, в ней удается проследить большое количество бифуркаций, приводящих к усложнению решения. Сделать это в более сложных моделях гораздо труднее. Как это ни удивительно, но пока встречались только циклы, период которых равен степени 2.

Чтобы понять, чем это вызвано, и изучить поведение модели более подробно, наряду с функцией f(x) удобно рассмотреть отображение f(f(х)), обозначаемое далее через f² (х), и вообще положить f^n+l (x) =f(fⁿ (x)), считая, конечно, что f(n) =f(х).

Построим график f(x).

Вот нужные нам определения.

Сначала рассмотрим случай устойчивой неподвижной точки. Вот что получим для случая г = 3.

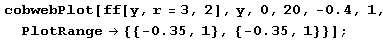
Теперь рассмотрим случай устойчивого цикла S².

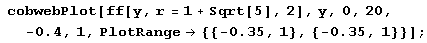
График функции f(x) пересекается с прямой у = х во всех неподвижных точках отображения / (ведь для любой неподвижной точки х отображения f имеем f² (х*) = f(f(x')) = f(x') = (х'), а также в точках, принадлежащих циклам 52 (потому что а2 = f(a1) = f(f(a2)) и а1 = f(a2) = f(f(f())) – Увеличивая параметр r, мы растягиваем функцию f(x) вдоль оси у. И если при некотором значении г линии у = х и у = fix) пересекаются в одной точке, то с увеличением г могут появиться еще две точки пересечения. Они-то и будут определять цикл S2.