Иллюстрированный самоучитель по Mathematica 5

Дробная часть вещественного числа (функция FractionalPart)

Теперь мы видим, что 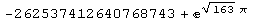действительно очень близко к целому числу 1, от него оно отличается менее, чем на 8x10^-13! Между прочим, когда системы компьютерной алгебры не были столь доступны, как сейчас, число е^√163π доставляло немало хлопот не только студентам, но и многим вполне серьезным "дядям и тетям", недостаточно знакомым с признаками трансцендентности чисел. Некоторые шутники с вполне серьезным видом заявляли, что все говорит о том, что число е является целым, но никто этого пока не доказал, и что за доказательство обещана кругленькая сумма и т.д.

А ведь чтобы прямым вычислением установить ложность этого высказывания, необходимо было провести вычисления более чем с 30 десятичными знаками! Даже вычислить его целую часть на машинах серии JBM/360 или БЭСМ-6 без ухищрений было невозможно! Конечно, на зарубежных машинах были доступны системы компьютерной алгебры, например MACSYMA на IBM/360. Однако на территории СССР доступ к таким системам имели весьма немногие. Кроме того, в советской системе образования следствием застойных явлений были ориентация на идеологические дисциплины (история КПСС, разнообразный марксизм и т.д.), отсутствие свободно выбираемых (студентом, а не деканатом!) курсов и сохранение подчиненной роли курса алгебры (всего три семестра) на уровне прошлого века. В советских университетах даже для студентов-математиков программой не было предусмотрено знакомство с современной алгеброй. О компьютерной алгебре не слышали и многие преподаватели. Поэтому на территории СССР вера в необходимость прямого вычисления с довольно большим количеством значащих цифр была не простым заблуждением обывателя, а подкреплялась советской системой образования. Поэтому именно те, кто был заинтересован в финансировании произвольноразрядной арифметики, и устраивали такие розыгрыши, предварительно тщательно выискивая потенциальных жертв.

Фактически из отечественных машин для проверки гипотезы подходили только машины серии МИР. Но машина МИР-1, во входном языке (Алмир) которой была реализована произвольноразрядная арифметика, имела память объемом всего лишь 4 Кбайт, а машина МИР-2-8 Кбайт, причем быстродействие машины МИР-2 из-за частой сборки мусора падало подчас до 200 операций в секунду! Тем не менее благодаря встроенному языку Аналитик, в котором была реализована произвольноразрядная арифметика и элементы компьютерной алгебры, она справлялась с задачами, одна лишь постановка которых на БЭСМ-6 была весьма трудоемка, и потому очередь к этой машине стояла в десятки раз больше, чем за колбасой. А поскольку заранее никто не мог сказать, сколько времени потребуется на вычисление, спланировать его не представлялось возможным. Что же касается машины МИР-3 (особенно модели МИР-32), то фактически она была доступна только разработчикам, из числа которых и находились самые злостные шутники! Кстати, в те годы системы компьютерной алгебры часто не могли определить, является ли заданное число алгебраическим. Начиная с версии 4 в системе Mathematica не составляет труда записать (и вычислить!) нужный предикат.

Всякая история имеет мораль, и эта не исключение: вычисляя дробную часть, не забывайте указывать нужную разрядность и, кроме того, не упускайте из виду цель, ради которой вы проводите вычисления, – подумайте, нельзя ли достичь цели более простым способом. (Мы бы, например, могли сразу спросить систему Mathematica, является ли е^{√163 π} алгебраическим числом.) Не забывайте также о том, что подчас с помощью систем компьютерной алгебры удается разрешить вопрос, который остается открытым в течение длительного времени. Впрочем, иногда достаточно вспомнить всего лишь несколько теорем.

Упражнение 3.1.
Вычислите не менее k десятичных цифр числа я, начиная с n-й после десятичной точки. Можете ли вы провести вычисления, например, для n = 100 000, k = 1000? Иными словами, можете ли вы вычислить сто первую тысячу (после запятой) знаков в представлении этого числа десятичной дробью?

Решение.
Вот самое простое решение, которое обычно приходит в голову неискушенному читателю. Сначала нужно вычислить п с разрядностью, которая гарантирует n + k + 1 верную цифру, например n + k + 10, а затем в полученной дроби выбрать нужные десятичные знаки. Что касается вычисления я с разрядностью хотя бы 101001, то оно для системы Mathematica никакого труда не представляет. Но вот что касается отсчитать сто тысяч знаков после запятой… Впрочем, в системе Mathematica и для этого предусмотрены нужные функции! Но если немного поразмыслить, то окажется, что решить поставленную задачу можно с помощью функции FractionalPart, "Ну, я об этом сразу догадался!" – высокомерно воскликнет искушенный читатель. Действительно, чего же можно было еще ожидать, если этот раздел посвящен функции FractionalPart? Ну разве что каких-либо трудностей при составлении программы. Но ее составить как раз совсем нетрудно.

Правда, ее нужно предварительно. проверить. Это совсем просто, достаточно уменьшить значения пик, затем провести вычисления:

И сверить результаты с таблицами.