Число как последовательность (список) цифр
А вот как узнать, насколько фактически эти цифры отличаются от среднего, 10n.
DigitCount[IntegerPart[10 ^ (10 ^ (n + 1)) * FractionalPart[N[E, 10 ^ (n + 1) + 10]]]] - 10 ^ n {1.1, -1, 0, -1, -1, 0, 3, -1, -1}А теперь посчитаем относительные отклонения от среднего.
N[(DigitCount[IntegerPart[10 ^ (10 ^ (n + 1)) * FractionalPart[N[E, 10 ^ (n + 1) + 10]]]] - 10 ^ n) / 10 ^ n, 4] {1.000.1.000, -1.000.0, -1.000, -1.000, 0, 3.000, -1.000, -1.000}Ну а теперь мы можем составить таблицу таких отклонений для n = 0, 1, 2, 3, 4, 5.

Одно время некоторых "цифроманов" очень беспокоили неравномерности в распределении девятки в десятичном представлении основания натуральных логарифмов. Честно говоря, просматривая эту таблицу, особых причин для беспокойства именно по поводу девятки я не вижу. Вы имеете возможность просмотреть таблицу, самостоятельно составить более подробную и сформировать собственное мнение – с помощью функции DigitCount это совсем просто! Если же изучать таблицу лень, можно представить данные в виде графика (обратите внимание на то, что ось, на которой отложены значения отклонений, не проходит через начало координат, которое находится вне графика).
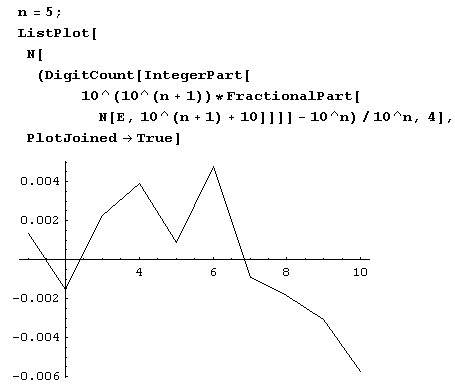
Из графика видно, что наибольшее отклонение от среднего в первом миллионе десятичных знаков не у девятки, а у нуля.
Аналогичный график для первых двух миллионов десятичных знаков строится так.
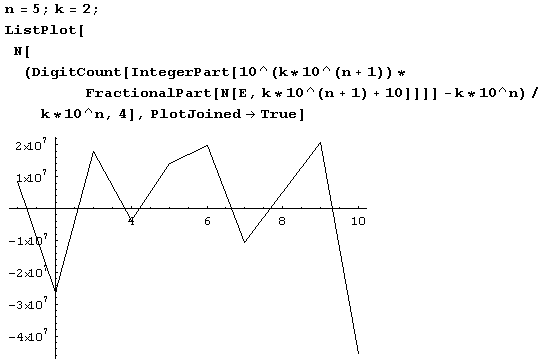
Как видите, если и винить, то скорее нули, а не девятки!
