Недостаточные, избыточные, совершенные и дружественные числа
Давайте найдем все избыточные нечетные числа, меньшие 100 000. Вот нужная нам программа.
Как видите, первым нечетным избыточным числом является 945. А избыточных нечетных чисел, меньших 100 000, всего 210. Это очень мало! Так что нам очень повезло: первое встреченное нами число оказалось избыточным нечетным. Остальные нечетные числа, меньшие 100 000, являются недостаточными. (Число, сумма всех делителей которого, не' считая самого числа, меньше самого числа, называется недостаточным. Иными словами, число л называется недостаточным, если о(n)<2и.) Как много бедных, как мало богатых… Ох, простите, я хотел сказать как много чисел недостаточных, как мало избыточных среди нечетных чисел, меньших 100 000. Если через А(х) обозначить число избыточных чисел, меньших или равных х, то 0.1241х<^(х)<0.314х, так что большинство чисел является недостаточным. Хотя существование предела отношения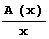 
было доказано еще в 1933 году, величина его до сих пор не определена.
А может ли последовательность х0 = a, n, = σ(n)-n,…, xn+1 = σ(xn)-nr1,… иметь период? Ведь если бы такое случилось, то, с точки зрения древних греков, этот период был бы "самодостаточным"! Известны случаи, когда эта последовательность вообще постоянна. Конечно, это происходит в том случае, если л – совершенное число. Но совершенных чисел так мало, а опасных, дальних дорог (хотя бы за золотым руном) так много! На все дороги не напастись совершенных чисел. Может быть, в такие дальние путешествия можно отправлять не только совершенные числа, но и периоды из таких последовательностей? С точки зрения древних греков, думаю, неплохая идея. Но длинные периоды – многочисленные экипажи. А для многочисленных экипажей нужны очень большие суда. Другое дело постоянные последовательности. У постоянных последовательностей длина периода равна 1. Но эти последовательности встречаются, как мы знаем, весьма редко. (Только отчаянные смельчаки могут рискнуть отправиться в дальнее одиночное плавание.) К тому же неизвестно, бесконечно ли их число.
Затем идут последовательности, у которых длина периода равна 2. Есть ли такие? Период таких последовательностей состоит всего из двух чисел, таких, что сумма делителей одного числа равна другому (напомним, что сами числа при подсчете суммы не учитываются). Фактически такой период является идеальной "супружеской" парой, в которой недостаток "чувств" (слагаемых) одного "супруга" (числа) компенсируется избытком "чувств" (слагаемых) другого. Такие пары чисел называются дружественными. Иными словами, пара (а, b) различных натуральных чисел афЬ называется дружественной, если о(n)-а = b, a a(b)-b -а. Увы, грекам не повезло: они знали лишь одну дружественную пару: 220 и 284. Лишь в 1636 году (письмо Мерсенну датировано 24 июня) Пьеру Ферма удалось найти еще одну: (17296, 18418). А сколько сможем найти мы? С помощью системы Mathematica, разумеется. Попробуем.