Жесткие системы ОДУ
Таким образом, во-первых, мы выяснили, что одни и те же уравнения с разными параметрами могут быть как жесткими, так и нежесткими. Во-вторых, чем жестче уравнение, тем больше шагов в обычных численных методах требуется для его устойчивого решения. С классическим примером ОДУ из листинга 11.11 все получилось хорошо, т. к. оно было не очень жестким, и небольшое увеличение числа шагов разрешило все проблемы. Для решения обычными методами более жестких уравнений требуются миллионы, миллиарды и даже большее число шагов.
Некоторые ученые замечают, что в последние годы методы Рунге-Кутты стали уступать свое главенствующее положение среди алгоритмов решения ОДУ методам, способным решать жесткие задачи.
Исторически, интерес к жестким системам возник в середине XX века при изучении уравнений химической кинетики с одновременным присутствием очень медленно и очень быстро протекающих химических реакций. Тогда неожиданно оказалось, что считавшиеся исключительно надежными методы Рунге-Кутты стали давать сбой при расчете этих задач. Рассмотрим классическую модель взаимодействия трех веществ (Робертсон, 1966), которая как нельзя лучше передает смысл понятия жесткости ОДУ.
Пусть вещество "0" – медленно превращается в "1": "0" › "1" (со скоростью 0.1), вещество "1" при каталитическом воздействии самого себя превращается очень быстро в вещество "2": "1" + "1" › "2" + "1" (10^3). И, наконец, подобным! образом (но со средней скоростью) реагируют вещества "2" и "1": "1" + "2" › "0" + "2" (10^2). Система ОДУ, описывающая динамику концентрации реагентов, с попыткой решения методом Рунге-Кутты, приведена в листинге 11.12.
Листинг 11.12. Жесткая система ОДУ химической кинетики:
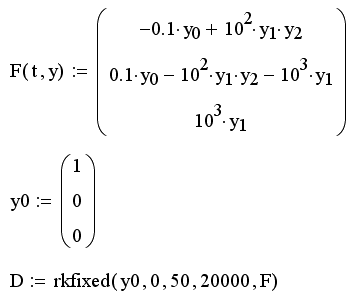
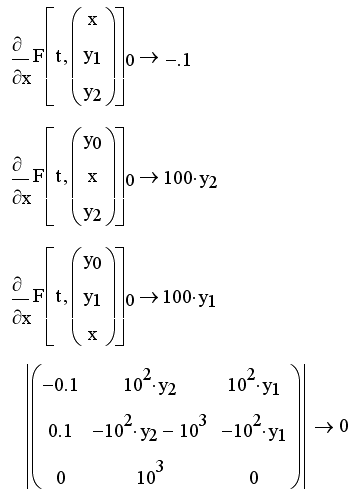
Бросается в глаза сильно различающийся порядок коэффициентов при разных слагаемых. Именно степень этого различия чаще всего и определяет жесткость системы ОДУ. В качестве соответствующей характеристики выбирают матрицу Якоби (якобиан) векторной функции F(t,у), т.е. функциональную матрицу, составленную из производных F(t,y) (см. разд. "Частные производные" гл. 7). Чем вырожденнее матрица Якоби, тем жестче система уравнений. В приведенном примере определитель якобиана и вовсе равен нулю при любых значениях у0, y1 и у2 (листинг 11.13, вторая строка). В первой строке листинга 11.13 приведено напоминание способа вычисления якобиана средствами Mathcad на примере определения элементов его первой строки.
Листинг 11.13. Якобиан рассматриваемой системы ОДУ химический кинетики:
