Формулы Шеннона для непрерывного и дискретного каналов
Под шумом понимается любой нежелательный сигнал, в том числе внешние помехи или сигнал, вернувшийся к передающему устройству – может быть, и модему – в результате отражения от противоположного конца линии. Сами по себе сосредоточенные помехи не столь существенно ограничивают пропускную способность аналогового канала, как непредсказуемый в каждый момент времени белый гауссовский шум. "Умные" высокоскоростные модемы умеют, как будет отмечено в дальнейшем, определять уровень и задержку "своих" отраженных сигналов и компенсировать их влияние.
Формула Шеннона для многопозиционного дискретного канала, построенного на базе предыдущего непрерывного канала, в отсутствие ошибок при приеме, имеет следующий вид:
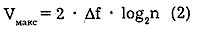
Здесь n – общее число вариантов дискретного (цифрового) сигнала (алфавит). Если за время одной посылки (длительность элементарного аналогового сигнала типа отрезка синусоиды) передается информация о k двоичных разрядах, то n = 2k. Практически расширение алфавита для дискретных сигналов приводит к появлению все менее различимых элементарных посылок, так что величина п ограничивается сверху все тем же отношением сигнал/шум S/N в аналоговом канале.
При учете ошибок при приеме формула Шеннона для многопозиционного дискретного канала, построенного на базе непрерывного канала, имеет следующий вид:
Здесь рош – отношение числа бит, принятых с ошибками, к общему числу переданных бит за время наблюдения, теоретически стремящееся к бесконечности, а практически достаточное для набора статистики.
Согласно стандарта МККТТ (CCITT, новое название той же организации – ITU-T), для телефонных сообщений должно выполняться условие рош. < 3 * 10-5, а для цифровых данных рош. < 10-6 (в отдельных случаях для критичных данных этот порог уменьшают до 10-9). При выполнении требований стандартов влиянием ошибок при приеме на максимально-допустимую скорость передачи можно полностью пренебречь и от соотношения (3) перейти к более простому соотношению (2). В частном случае бинарного канала (k = 1, n = 2) при Рош= 1/2 из соотношения (3) следует, что V – 0, а при р › 0 и при р › 1 V › 2 * Af.
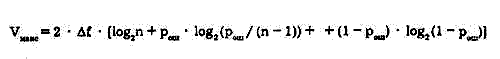
Физический смысл такой зависимости состоит в том, что при рош– 1/2 принятый сигнал не содержит полезной информации (каждый из принятых битов может оказаться ошибочным). При рош (гипотетический случай, имеющий чисто теоретический интерес) каждый бит с большой вероятностью инвертируется, и доля полезной информации снова возрастает.
Формулы Шеннона показывают, что наиболее эффективный способ увеличения максимальной скорости передачи Умакс состоит в увеличении полосы пропускания линии передачи Af (VMaKc ~ Af). Логарифмическая зависимость VMaKc от отношения сигнал/шум S/N делает этот путь повышения Умакс гораздо менее перспективным и более трудоемким. Однако на практике редко возможен свободный выбор линии передачи, который с точки зрения реализации максимальной скорости передачи однозначно сводится к использованию оптоволоконной линии связи (ВОЛС). Суровая действительность часто состоит в том, что имеется телефонная линия, по которой и нужно организовать передачу с использованием модемов.
Как уже говорилось, телефонная линия (точнее, тракт передачи, функционирующий на этой линии, с учетом фильтров) имеет фиксированную полосу пропускания Af = 3400-300 = 3100 Гц, поэтому приходится бороться именно за повышение отношения сигнал/шум. Да и то хороший результат сам по себе не гарантирован, так как речь идет о реализации возможностей, близких к теоретическому пределу. Практический предел отношения сигнал/ шум в аналоговой телефонной линии составляет примерно 35 дБ (более 3000 раз по мощности или более 56 раз по амплитуде), что соответствует максимальной скорости VMBKC – 34822 бит/сек (стандартное значение, реализуемое на практике, 33600 бит/сек). Популярные в настоящее время 56К-модемы реализуют заявленную скорость только в одну сторону – от провайдера (из сети) до пользователя и только при условии работы провайдера непосредственно на цифровой, несколько более широкополосной, линии передачи (чудес не бывает!).