Введение в двоичную арифметику
Пример 1.1. Сложение двух 8-разрядных чисел (83 + 56 = 139).
| 1 | 1 | перенос | |||||||
| + | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1-е слагаемое |
| - | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 2-е слагаемое |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | результат |
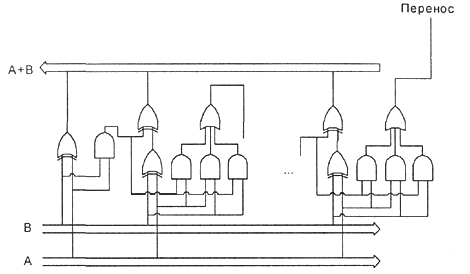
Рис. 1.1. 8-разрядный двоичный сумматор
Дополнительный, 9-й разряд, образующийся при сложении 8-разрядных чисел, переносится в специальный бит слова состояния процессора, который также называется битом переноса, и обычно обозначается буквой С (от англ, саrrу – перенос). Этот бит можно использовать как условие в командах условного перехода, а также для реализации 16-разрядной операции сложения или одноименной операции большей разрядности на 8-разрядном АЛУ.
При операциях над беззнаковыми (неотрицательными) числами бит переноса можно интерпретировать как признак переполнения: т. е. того, что результат нельзя представить числом с разрядностью АЛУ. Игнорирование этого бита может приводить к неприятным последствиям: например, складывали мы 164 + 95, а получили в результате 3.
Иногда этот эффект, называемый "оборачиванием счетчиков", имеет и полезное применение. Например, используя "часовой" кварцевый генератор с частотой 32 768 Гц и 15-разрядный двоичный счетчик, мы можем отмерять секунды по появлению бита переноса в 16-м разряде и избавляемся от необходимости сбрасывать сам счетчик.
Двоичное вычитание может выполняться аналогичным образом, только необходимо использовать не таблицы сложения, а таблицы вычитания для двух и трех слагаемых. Не утомляя себя и читателя выписыванием этих таблиц, скажем сразу, что операция двоичного вычитания эквивалентна операции двоичного сложения уменьшаемого с двоичным дополнением вычитаемого. Двоичное дополнение строится таким образом: все биты числа инвертируются (нули заменяются на единицы, и наоборот), а затем к результату добавляется единица. Доказательство этого утверждения мы оставляем любопытному читателю, а сами просто рассмотрим пример 1.2.
Пример 1.2. Вычитание чисел (83-56 = 27).
Построение двоичного дополнения 56:
| 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | число |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | побитовое отрицание |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | побитовое отрицание+1 |
Сложение с двоичным дополнением (83 + 56) mod 256 = 27:
| 1 | 0 | |||||||
| + | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| - | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
