Введение в двоичную арифметику
Подавляющее большинство современных процессоров использует двоично-дополнительное представление для целых чисел. В те времена, когда компьютеры были большими, встречались системы, применявшие для этой цели дополнительный, знаковый бит: число -1 представлялось так же, как +1, но с установленным знаковым битом. Такие процессоры должны были иметь отдельные команды для беззнаковых и знаковых арифметических операций и более сложное АЛУ. Кроме того, при таком представлении возникает специфическая проблема "отрицательного нуля".
Иногда наравне с двоичным используется и специфическое, так называемое двоично-десятичное представление чисел (рис. 1.2). Это представление особенно удобно для приложений, которые постоянно вынуждены использовать десятичный ввод и вывод (микрокалькуляторы, часы, телефоны с автоопределителем номера и т. д.) и имеют небольшой объем программной памяти, в который нецелесообразно помещать универсальную процедуру преобразования чисел из двоичного представления в десятичное и обратно.
В таком представлении десятичная цифра обозначается тетрадой, четырьмя битами. Цифры от 0 до 9 представляются 0, 1111 недопустимы.своими двоичными эквивалентами, а комбинации битов 1010, 1011, 1100, 1101, 111.
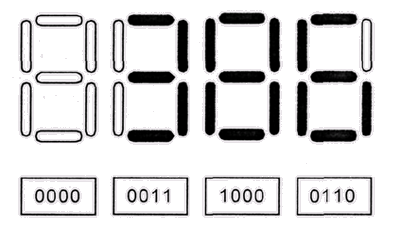
Рис. 1.2. Двоично-десятичное представление чисел
Вместо арифметических операций над такими числами большинство современных микропроцессоров предлагают использовать для их сложения и вычитания обычные бинарные операции, а потом исправлять возникающие при этом недопустимые значения при помощи специальной команды двоично-десятичной коррекции. Алгоритм работы этой команды читателю предлагается разработать самостоятельно. Для него потребуется информация о том, происходил ли при сложении двоичный перенос из младшей тетрады. Процессоры, предоставляющие такую команду, имеют и бит межтетрадного переноса.
Если операция производится над числами, имеющими 16 или более двоичных разрядов (4 и более двоично-десятичных), для коррекции нам недостаточно одного межтетрадного переноса – надо иметь по биту переноса на каждую из пар последовательных тетрад. Так далеко ни один из существующих процессоров не заходит. Например, 32-разрядные процессоры х86 имеют команды двоично-десятичной коррекции только для операций над числами с 8-ю двоичными (двумя двоично-десятичными) разрядами.
