Алгоритмы динамического управления памятью
Чем больше размер единицы выделения, тем меньше нам грозит фрагментация внешняя, и тем большие потери обеспечивает фрагментация внутренняя. Величина потерь зависит от среднего размера запрашиваемого блока. Грубая оценка свидетельствует о том, что в каждом блоке в среднем теряется половина единицы выделения, т. е. отношение занятой памяти к потерянной будет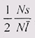 
, где N– количество выделенных блоков, s– размер единицы выделения, а 
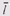– средний размер блока. Упростив эту формулу, мы получим выражение для величины потерь: 
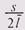,т. е. потери линейно растут с увеличением размера единицы выделения.
Если средний размер блока сравним с единицей выделения, наша формула теряет точность, но все равно дает хорошую оценку порядка величины потерь. Так, если s =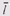, наша формула дает 50% потерь, что вполне согласуется Со здравым смыслом: если запрашиваемый блок чуть короче минимально возможного, теряется только это "чуть"; зато если он чуть длиннее, то для него отводится два минимальных блока, один из которых теряется почти весь. Точная величина потерь определяется распределением запрашиваемых блоков по длине, но мы предпочитаем оставить вывод точной формулы любопытному читателю.
Варианты алгоритмов распределения памяти исследовались еше в 50-е году. Итоги многолетнего изучения этой проблемы приведены в [Кнут 2000] и многих других учебниках.
Обычно все свободные блоки памяти объединяются в двунаправленный связанный список. Список должен быть двунаправленным для того, чтобы из него в любой момент можно было извлечь любой блок. Впрочем, если все действия по извлечению блока производятся после поиска, то можно слегка усложнить процедуру поиска и всегда сохранять указатель на предыдущий блок. Это решает проблему извлечения и можно ограничиться однонаправленным списком. Беда только в том, что многие алгоритмы при объединении свободных блоков извлекают их из списка в соответствии с адресом, поэтому для таких алгоритмов двунаправленный список остро необходим.
Поиск в списке может вестись тремя способами: до нахождения первого подходящего (first fit) блока, до блока, размер которого ближе всего к заданному – наиболее подходящего (best fit), и, наконец, до нахождения самого большого блока, наименее подходящего (worst fit).
Использование стратегии worst fit имеет смысл разве что в сочетании с сортировкой списка по убыванию размера. Это может ускорить выделение памяти (всегда берется первый блок, а если он недостаточно велик, мы с чистой совестью можем сообщить, что свободной памяти нет), но создает проблемы при освобождении блоков: время вставки в отсортированный список пропорционально О(n), где n – размер списка.
Помещать блоки в отсортированный массив еще хуже – время вставки становится О(n + log(n)) и появляется ограничение на количество блоков. Использование хэш-таблиц или двоичных деревьев требует накладных расходов и усложнений программы, которые себя в итоге не оправдывают. На практике стратегия worst fit используется при размещении пространства в файловых системах, например в HPFS, но ни одного примера ее использования для распределения оперативной памяти автору неизвестно.
Чаще всего применяют несортированный список. Для нахождения наиболее подходящего мы обязаны просматривать весь список, в то время как первый подходящий может оказаться в любом месте, и среднее время поиска будет меньше. Насколько меньше – зависит от отношения количества подходящих блоков к общему количеству. (Читатели, знакомые с теорией вероятности, могут самостоятельно вычислить эту зависимость.)
В общем случае best fit увеличивает фрагментацию памяти. Действительно, если мы нашли блок с размером больше заданного, мы должны отделить "хвост" и пометить его как новый свободный блок. Понятно, что в случае best fit средний размер этого "хвоста" будет маленьким, и мы в итоге получим большое количество мелких блоков, которые невозможно объединить, так как пространство между ними занято.
В тех ситуациях, когда мы размещаем блоки нескольких фиксированных размеров, этот недостаток роли не играет и стратегия best fit может оказаться оправданной. Однако библиотеки распределения памяти рассчитывают на обший случай, и в них обычно используются алгоритмы first fit. При использовании first fit с линейным двунаправленным списком возникает специфическая проблема.
Если каждый раз просматривать список с одного и того же места, то большие блоки, расположенные ближе к началу, будут чаще удаляться. Соответственно, мелкие блоки будут скапливаться в начале списка, что увеличит среднее время поиска (рис. 4.6). Простой способ борьбы с этим явлением состоит в том, чтобы просматривать список то в одном направлении, то в другом. Более радикальный и еще более простой метод заключается в следующем: список делается кольцевым, и каждый поиск начинается с того места, где мы остановились в прошлый раз. В это же место добавляются освободившиеся блоки. В результате список очень эффективно перемешивается и никакой "антисортировки" не возникает.
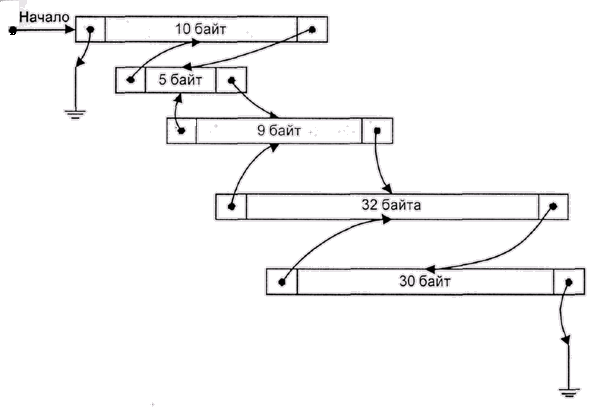
Рис. 4.6. Антисортировка