Улучшение классических методов сортировки
Сортировка с помощью дерева
Следующий алгоритм (программа prgl0_229.asm) является улучшением сортировки прямым выбором. Автор алгоритма сортировки с помощью дерева – Дж. У. Дж. Уильяме (1964 год). В литературе этот алгоритм носит название "пирамидальной" сортировки. Если обсужденные выше сортировки интуитивно понятны, то алгоритм данной сортировки необходимо пояснить подробнее. Этот алгоритм предназначен для сортировки последовательности чисел, которые являются отображением в памяти дерева специальной структуры – пирамиды. Пирамида – помеченное корневое двоичное дерево заданной высоты h, обладающее тремя свойствами:
- каждая конечная вершина имеет высоту h или h-1;
- каждая конечная вершина высоты h находится слева от любой конечной вершины высоты h-1;
- метка любой вершины больше метки любой следующей за ней вершины.
На рис. 2.3 изображено несколько деревьев, из которых лишь одно Т4 является пирамидой.
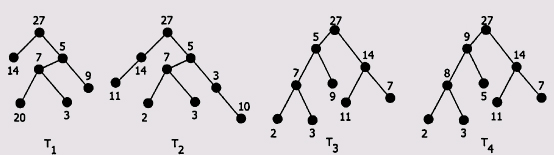
Рис. 2.3. Примеры деревьев (Т4 – пирамида)
Такая структура пирамид позволяет компактно располагать их в памяти. Например, пирамида, показанная на рисунке, в памяти будет представлена следующим массивом: 27, 9, 14, 8, 5, 11, 7, 2, 3. Оказывается, что такая последовательность чисел легко подвергается сортировке.
Таким образом, сортировка массива в соответствии с алгоритмом пирамидальной сортировки осуществляется в два этапа: на первом этапе массив преобразуется в отображение пирамиды; на втором – осуществляется собственно сортировка. Соответственно нами должны быть разработаны две процедуры для выполнения задач каждого из этих двух этапов.
ПРОЦЕДУРА insert_item_in_tree (i .mas. N) // //insert_item_in_tree – процедура на псевдоязыке вставки элемента на свое место в пирамиду //Вход: mas[n] – сформированная не до конца пирамида: 1 – номер добавляемого элемента :в пирамиду из mas[n] (с конца): n – длина пирамиды //Выход: действие – элемент добавлен в пирамиду. НАЧ_ПРОГ j: = i @@ml: k: = 2*j: h-k+1 ЕСЛИ (1=<N И (mas[j]<mas[k] ИЛИ mas[j]<mas[l]) TO ПЕРЕЙТИ_НА @йп6 ИНАЧЕ ПЕРЕЙТИ_НА @@m2 КОН_ЕСЛИ @@m6: ЕСЛИ tnas[k]>mas[l] TO ПЕРЕЙТИ_НА @@т4 ИНАЧЕ ПЕРЕЙТИ_НА @@тЗ КОН_ЕСЛИ @@т4: x: = mas[j] mas[j]: = mas[k] j: = k mas[k]: = x ПЕРЕЙТИ_НА (a0ml (а@тЗ: x: = mas[j] mas[j]: = mas[l] mas[l]: = x ПЕРЕЙТИ_НА @@ml* @@m2: ЕСЛИ (k==n И mas[j]<mas[k]) TO ПЕРЕЙТИ_НА @@m7 ИНАЧЕ ПЕРЕЙТИ_НА @@m8 КОН_ЕСЛИ @@m7: x: = mas[j] mas[j]: = mas[n] ;m-n/2 – значение, равное половине числа элементов массива mas push si push ex movj.si:j\>>1 @@m4: movsi.j:i › si movax.j:k: = 2*j; l:-k+l shlax.l:j*2 movk.ax: k: = j*2 inc ax movl.ax:l:"k+l cmpax.m:l<m ja @@m2 moval,raas[si-l];ax:-mas[j] mov di,k emp al,mas[di-l] jna @@m6 inc di emp al.mas[di-l] jna @@m6 jmp @@m2 @@m6:;условие выполнилось: ;2j+l+<M AND (mas[j]<mas[2j] OR mas[j]<mas[2j+l]):обмен с mas[j] mov di,k mov al,mas[di-1];ax: = mas[k] inc di emp al,mas[di-l]:mas[k]>mas[l] jna ШтЗ mov al,raas[si-l] movx.al;x: = rnas[j] dec di mov al,mas[di-l] movmas[si-l].al:mas[j]: = mas[k] movj.di:j: = k mov al.x movmas[di-l],al:mas[k]: = x jmp @?m4 :@@m3: x: = mas[j];ПЕРЕЙТИ_НА @@ml №m3::mas[k] =< mas[l] mov al,mas[si-l] movx.al:x: = mas[j] mov al,mas[di-l] movmas[si-l].al;mas[j]: = mas[l] movj.di:j: = l mov al,x movmas[di-l].al;mas[l]: = x jmp @@m4 Шт2:; условие не выполнилось: 2j+l+<M AND (mas[j]<mas[2j] OR mas[j]<mas[2j+l]) mov ax.k emp ax.m
