Сеть
Неважно, что кто-то идет неправильно, возможно, это хорошо выглядит…
Первый закон Скотта
(Прикладная Мерфология)
Выше мы уделили достаточно внимания работе с матрицами и списками, и это сделано не случайно. Еще более обобщая понятие списка, мы придем к определению многосвязного списка, для которого характерно наличие произвольного количества указателей на другие элементы списка. Можно говорить, что каждый конкретный элемент входит в такое количество односвязных списков, сколько у него есть указателей. Многосвязный список получается "прошитым" односвязными списками, поэтому такие многосвязные списки называют прошитыми, или плексами. С помощью многосвязных списков можно моделировать такую структуру данных, как сеть или граф. Частный случай сети – дерево. Рассмотрим варианты представления в памяти компьютера этих структур данных.
Сетью называется кортеж G -(V,E), где V – конечное множество вершин, Е – конечное множество ребер, соединяющих пары вершин из множества V. Две вершины и и v из множества V называются смежными, если в множестве Е существует ребро (u, v), соединяющее эти вершины. Сеть может быть ориентированной и неориентированной. Это зависит от того, считаются ли ребра (u, v) и (v, u) разными. В практических приложениях часто ребрам приписываются веса, то есть некоторые численные значения. В этом случае сеть называется взвешенной. Для каждой вершины v в сети есть множество смежных вершин, то есть таких вершин Uj (i = l..n), для которых существуют ребра (v, и:). Это далеко не все определения, касающиеся сети, но для нашего изложения их достаточно, так как его цель – иллюстрация средств ассемблера для работы с различными структурами данных.
Поэтому рассмотрим варианты представления сетей в памяти компьютера в виде, пригодном для обработки. Какой из этих вариантов лучше, зависит от конкретной задачи. Мы также не будем проводить оценку эффективности того или иного вида представления.
Матрица смежности.
Сеть, имеющую М вершин, можно представить в виде матрицы размерностью МхМ. При условии, что вершины помечены v,, v2,…, vm, значение матрицы ау = 1 говорит о существовании ребра между вершинами v, и v,. Иначе говоря, эти вершины являются смежными. Для ориентированной сети матрица смежности будет симметричной.
Матрица инцидентности.
В основе этого представления также лежит матрица, но строки в ней соответствуют вершинам, а столбцы – ребрам (рис. 2.15). Из рисунка видно, что каждый столбец содержит две единицы в строках, причем одинаковых столбцов в матрице нет.
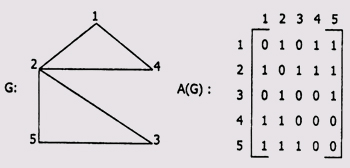
Рис. 2.15. Представление сети матрицей инцидентности
Векторы смежности.
Этот вариант представления также матричный (рис. 2.16). Все вершины пронумерованы. Каждой вершине соответствует строка матрицы, в которой перечислены номера вершин, смежных с данной.
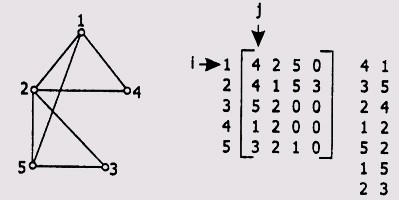
Рис. 2.16. Представление сети векторами смежности