Дерево
Представление дерева в памяти
Естественным является представление дерева в памяти компьютера в форме многосвязного списка. Это наиболее динамичное представление. В случае постоянства структуры дерева могут использоваться и другие способы представления дерева в памяти, например в виде массива, как это было во время рассмотрения нами двоичной сортировки. В случае представления дерева в форме многосвязного списка указатель на начало списка должен указывать на элемент списка, являющийся корнем. В свою очередь, узлы дерева связываются между собой так, чтобы корень дерева был связан с корнями его поддеревьев и т. д. При этом можно выделить три случая.
- Связь узлов в дереве осуществляется таким образом (рис. 2.19, а), что каждый узел-сын содержит ссылку на вышестоящий узел (узел-отца). В этом случае корень будет содержать нулевой указатель на месте соответствующего указателя. Имея такой тип связей узлов в дереве, можно подниматься от нижних уровней дерева к его корню, что может быть полезным при реализации определенных видов синтаксического разбора.
- Каждый узел дерева содержит указатели на свои поддеревья (рис. 2.19, б), то есть каждый отец ссылается на своих сыновей. Этот способ применим для представления деревьев небольшой m-арности, например бинарных деревьев. Имея указатель на корень дерева, можно достичь любого узла дерева.
- Каждый узел дерева ссылается на свои поддеревья с помощью списка, при этом каждый узел содержит два указателя – для представления списка поддеревьев и для связывания узлов в этот список (рис. 2.19, е).
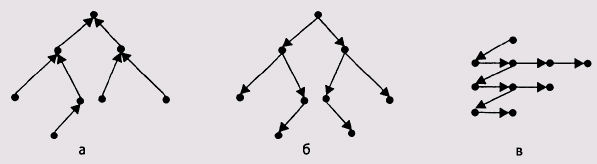
Рис. 2.19. Варианты связи узлов дерева между собой
Бинарное дерево обычно представляется с помощью второго способа (рис. 2.19, б). Минимально для представления узла достаточно трех полей: содержательной части узла и двух указателей – на левого (старшего) и правого (младшего) сыновей. Таким образом, представить бинарное двоичное дерево можно с помощью нелинейного двусвязного списка. Структуру узла в программе можно описать так:
node_tree struc;узел дерева simbol db 0 содержательная часть l_son dd 0 указатель на старшего (левого) сына r_son dd 0 указатель на младшего (правого) сына ends
Рассмотрим на простом примере реализацию основных операций над деревом. Ранее при обсуждении сортировок упоминался двоичный поиск. При этом говорилось, что сам алгоритм совпадает с алгоритмом прохождения пути от вершины двоичного дерева к заданной его вершине. Реализуем этот вид поиска, но уже с использованием действительно двоичного дерева. Для начала построим двоичное дерево, используя произвольный массив чисел.
Построение двоичного дерева
Как уже отмечалось выше, для реализации двоичного поиска необходим упорядоченный массив чисел. Поэтому уже на этапе построения двоичное дерево необходимо специальным образом организовать. Двоичное дерево поиска организуется так, что между его узлами существуют следующие соотношения: для каждого узла а, все элементы левого поддерева меньше а, а элементы правого поддерева больше либо равны а.
:prg02_12.asm – программа построения и инициализации двоичного дерева. :Вход: произвольный массив чисел в памяти. :Выход: двоичное дерево в памяти. ;объявления структур: node_tree struc:узел дерева simbol db 0 содержательная часть l_son dd 0 указатель на старшего (левого) сына r_son dd 0 указатель на младшего (правого) сына ends .data mas db 37h.12h.8h.65h.4h.54h.11h.02h.32h.5h.4h.87h.7h.21h.65h.45h.22h. Ilh,77h.51h,26h.73h.35h.l2h.49h.37h.52h l_mas=$-mas .code BuildBinTree proc формируем корень дерева и указатель на дерево HeadTree :для размещения дерева используем кучу, выделяемую процессу по умолчанию (1 Мбайт). :но при необходимости можно создать и доп. кучу с помощью HeapCreate iHANDLE GetProcessHeap (VOID): call GetProcessHeap movHand_Head,eax сохраняем дескриптор ;запрашиваем и инициализируем блок памяти из кучи для корня дерева: xorebx.ebx:здесь будет указатель на предыдущий узел
