Улучшение классических методов сортировки
ПРОГРАММА prg27_136 //prg27_136 (по Кнуту) – программа на псевдоязыке "быстрой сортировки" массива. //Вход: mas[n] – неупорядоченная последовательность двоичных значений длиной п. //Выход: mas[n] – упорядоченная последовательность двоичных значений длиной n. ПЕРЕМЕННЫЕ INTJYTE n: //длина mas[n] INT_BYTE mas[n]; //сортируемый массив размерностью п (О..п-1) INTJYTE К; TEMP: i=0; j=0: 1=0: г=0; // i .j. 1. г – индексы INT_WORD M=l //длина подпоследовательности, для которой производится сортировка методом прямых включений //для отладки возьмем М=1 НАЧ_ПРОГ ЕСЛИ M<N TO ПЕРЕЙТИ_НА q9 1:-1: г: = п ВКЛЮЧИТЬ_В_СТЕК (Offffh) //Offffh – признак пустого стека q2: i:-l: j:-r+l: k: = mas[l] q3: ЕСЛИ i=<j-l TO ПЕРЕЙТИ_НА qq3 ПЕРЕЙТИ_НА q4 //итерация прекращена qq3: i: = i+l ЕСЛИ mas[i]<K TO ПЕРЕЙТИ_НА q3 q4: j:-j-l ЕСЛИ j<1 TO ПЕРЕЙТИ_НА q5 ЕСЛИ K<mas[j] TO ПЕРЕЙТИ_НА q4 ЕСЛИ j>i TO ПЕРЕЙТИ_НА q6 Iq2:;1:-1: j:-r+l: k:-nas[l] movsi.L;i(si): = L mov di. R incdi;j(di) : = R+l xor ax.ax mov al,mas[si] mov k.al q3::ЕСЛИ 1-sj-l TO ПЕРЕЙТИ_НА qq3 inc si;i: = i+l cmp si.di:i=<j jleqq3 dec si:сохраняем i=<j jmp q4:ПЕРЕЙТИ_НА д4//итерация прекращена qq3: moval.k;i: = i+l cmpmas[si].al:ЕСЛИ mas[i]<K TO ПЕРЕЙТИ_НА q3 jb q3 q4: decdi;j: = j-l cmpdi.si:j>=i-l jb q5 mov al,k:ЕСЛИ K<mas[j] TO ПЕРЕЙТИ_НА q4 cmp al,mas[di] >>jb q4 q5:;ЕСЛИ j>i TO ПЕРЕЙТИ_НА q6 cmpdi.si:j=<i??? J9 q6 movbx.L: //обмен mas[l]: = mas[j] mov dl,mas[bx] xchg mas[di].dl xchg mas[bx].dl jmpq7: ПЕРЕЙТИ_НА q7 q6: mov dl.masCsi]; mas[i]< › mas[j] xchg mas[di].dl xchg mas[si].dl jmpq3; ПЕРЕЙТИ_НА q3 q7:;ЕСЛИ r-j>j-l>M TO mov ax,г subax.di;r-j › ax mov bx.di subbx.l:j-l › bx cmpax.bx:r-j>j-l??? jl q7_m4 cmpbx.M;j-l>M??? jleq7_m3;1, r-j>j-l>M – в стек (j+l.r); r: = j-l; перейти на шаг q2 mov ax.di inc ax push ax (push г mov r.di dec г:г: = j – 1 q7_m4:;r-j>M??? cmp ax.M jg q7_m2 cmp bx. M jleq8;4 .j-l>M>r-j – r: = j-l: перейти на шаг q2 mov r.di dec г jmpq2 q7_m3: cmpax.M jleq8;3 .r-j>M>j-l – l: = j+l: перейти на шаг q2 mov 1,di inc 1 jmpq2 q7_m2::2 .j-l>r-j>M – в стек (l.j-1); l: = j+l; перейти на шаг q2 push 1 mov ax.di inc ax push ax mov 1,di inc 1 jmpq2 q8: извлекаем из стека очередную пару (l.r) pop г cmpr.Offffh:ЕСЛИ r<>0ffffh TO ПЕРЕЙТИ_НА q2 je q9 pop! jmpq2 q9: ;сортировка методом прямых включений – при М=1 этот шаг можно опустить (что и сделано для экономии места)
Обратите внимание на каскад сравнений шага q7, целью которых является проверка выполнения следующих неравенств:
- r-j>=j-1>M – в стек (j+l,r); r:-j-1; перейти на шаг q2;
- j-1>r-j>M – в стек (1, j-1); I: = j+1; перейти на шаг q2;
- r-j>M>j-1 – 1: = j+1; перейти на шаг q2;
- j-1>M>r-j – г: = j-1; перейти на шаг q2.
Проверка этих неравенств реализуется в виде попарных сравнений, последовательность которых выглядит так, как показано на рис. 2.4.
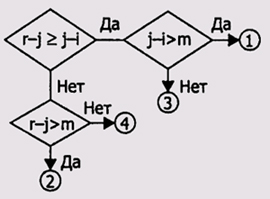
Рис. 2.4. Последовательность сравнений шага q7
За подробностями алгоритма можно обратиться к тому 3 "Сортировка и поиск" книги Кнута.
Существует другой вариант алгоритма этой сортировки – у Вирта в книге "Алгоритмы + структуры данных – программы" [4]. Но у него используется понятие медианы последовательности. Задачу нахождения медианы мы рассматривали выше. Эта задача интересна еще и тем, что она, по сути, является одной из задач поиска, рассмотрению которых посвящен следующий раздел.
