Массивы структур – таблицы
В этой программе показаны основные приемы работы с неупорядоченной таблицей. Усложнить данную программу можно, например, дополнив набор сведений о каждой константе информацией о ее длине. Далее можно попрактиковаться в этом вопросе, поставив себе задачу удалить из таблицы данные о нулевых константах (обоих типов – 0 и 0h) и вывести окончательное содержимое таблицы на экран. В качестве ключа для доступа к ячейке таблицы можно использовать значение самой константы (размером 10 байт).
Обратите внимание на еще два момента, отраженные в этой программе.
- Использование команды XLAT для классификации символов в качестве цифр и остальных символов (букв). Среди других кодов в таблице перекодировки особо выделен байт со значением Odh, который является первым байтом в паре OdOah. Как вы помните, эта пара вставляется редакторами ASCII-текстов для обозначения конца строки и перехода на другую строку.
- Организация таблицы. Ей предшествует четырехбайтовый префикс, содержащий информацию о конце таблицы и первом свободном элементе таблицы. В целях оптимизации область памяти для буфера buf и таблицы перекодировки лучше выделять динамически и после анализа файла удалять.
Древовидные таблицы
Древовидные таблицы являются несколько улучшенным вариантом неупорядоченных таблиц. Новые записи в древовидную таблицу по-прежнему поступают неупорядоченно. Но на этот раз место, занимаемое этими записями среди других записей в таблице, определяется значением ключевого поля. Принцип здесь такой же, как и в сортировке с помощью дерева (см. материал выше).
В общем случае каждая запись в древовидной таблице сопровождается двумя указателями (рис. 2.7): один указатель хранит адрес записи с меньшим значением ключа (адрес узла-предка), второй – с большим (адрес узла-сына).
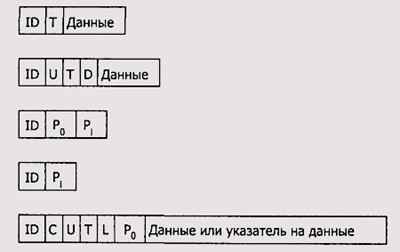
Рис. 2.7. Древовидная организация таблицы
Процесс добавления нового элемента в древовидную таблицу производится следующим образом. Значение ключа нового элемента сравнивается со значением ключа первого элемента дерева. По результатам сравнения ключей новый элемент "поступает" в левое или правое поддерево первого элемента дерева. Далее процесс сравнения и поступления в левое или правое поддерево очередного узла продолжается аналогичным образом и до тех пор, пока не будет найден пустой элемент в нужном направлении просмотра. Новая запись помещается в данный пустой элемент, при этом настраивается указатель с адресом узла-предка.
Преимущества древовидной структуры таблицы проявляются на этапе поиска нужного элемента. Сам процесс подобен действиям на этапе вставки нового элемента в таблицу, являясь при этом в отличие от неупорядоченного поиска целенаправленным. Поиск прекращается либо при совпадении ключевого поля, либо при обнаружении пустого указателя, то есть это означает, что нужного элемента в таблице нет.
Самое сложное в использовании древовидных таблиц – реализация процесса удаления элементов, так как при этом необходимо производить их переупорядочивание.
Реализовать таблицу древовидной организации можно как с использованием полей указателей (см. выше), так и без них. Если отказаться от полей указателей, то таблица может представлять собой массив из п структур, которые пронумерованы от 0 до n-1. Тогда структура с ключом, соответствующим корню дерева, должна располагаться на месте структуры с номером m = [(n-1)/2], где скобки [] означают целую часть от деления. Соответственно левое поддерево будет располагаться в левом подмассиве (элементы 0..m-1), а правое – в правом подмассиве (элементы m+1..n-1). Корень левого поддерева – элемент ш,' – [(m-1)/2], корень правого поддерева – элемент mr = [т+1+(п-1)/2] и т. д. Этот способ экономичнее с точки зрения расходования памяти, но сложнее алгоритмически. Предполагается, что соответствующее таблице дерево сбалансировано и максимальное количество элементов в таблице известно.
Наглядный пример организации древовидной таблицы – расстановка слов в лексикографическом порядке. Эта операция выполняется с помощью лексикографических деревьев, понятие о которых приведено ниже – в разделе, посвященном деревьям. Там же приведен соответствующий пример.