CRC-арифметика
Операцию вычитания демонстрирует следующий пример:
| 11111011 | |
| 11001010 | |
| 00110001 |
Правила выполнения вычитания в арифметике с отсутствием переносов: 0-0=0; 0-1=1; 1-0=1; 1-1=0.
Сравнение примеров для сложения и вычитания полиномов по модулю 2, а также правил, по которым они выполняются, показывает то, что эти две операции CRC-арифметики идентичны и по принципу формирования результата они аналогичны команде ассемблера XOR. Цель, которой достигают всеми этими условностями, – исключить из поля внимания все величины (путем заемов/переносов), лежащие за границей старшего разряда.
Умножение в арифметике с отсутствием переносов также выполняется с учетом особенностей CRC-сложения:
| 1101 | |||
| x | 1011 | ||
| 1101 | |||
| 1101 | |||
| 0000 | |||
| 1101 | |||
| 1111111 | |||
Видно, что в самом умножении особенностей нет, а вот сложение промежуточных результатов производится по правилам CRC-сложения.
Для нашего рассмотрения особый интерес представляет операция деления, так как в основе любого алгоритма вычисления CRC лежит представление исходного сообщения в виде огромного двоичного числа, делении его на другое двоичное число и использовании остатка от этого деления в качестве значения CRC. Деление – самая сложная из операций CRC-арифметики.
Здесь необходимо ввести так называемое слабое понятие размерности: число X больше или равно числу Y, если оба числа имеют одинаковую размерность и позиции их старших битов единичны, то есть соотношение остальных битов X и Y для операции сравнения не имеет значения. Рассмотрим примеры операции деления, причем для лучшего понимания сделаем это в двух вариантах: вначале вспомним, как выполняется обычное деление (по правилам двоичной арифметики с циклическим переносом), а затем выполним собственно CRC-деление.
Возьмем произвольную двоичную последовательность и разделим ее на некоторое число по правилам двоичной арифметики с циклическим переносом (рис. 9.3).
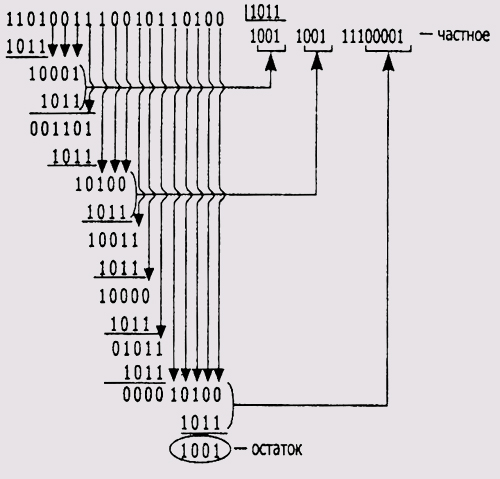
Рис. 9.3. Схема вычисления двоичного деления (с циклическим переносом)
