CRC-арифметика
По правилам CRC-арифметики деление для приведенных выше исходных данных даст следующий результат (рис. 9.4).
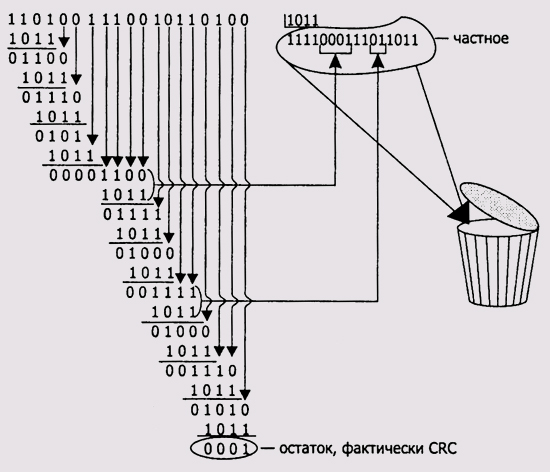
Рис. 9.4. Схема вычисления CRC-деления
Как видите, результаты обычного и CRC-делений отличаются. Главное, чтобы вы подметили особенность выполнения CRC-деления. Особое внимание обратите на порядок формирования промежуточных результатов в процессе деления. Снос двоичных разрядов из делимого продолжается до тех пор, пока размерности промежуточного битового значения и делителя не сравняются, а их старшие разряды не станут равными 1. После этого над двоичными разрядами выполняется побитовое CRC-вычитание.
Соотношение разрядов не важно, главное – это одинаковая размерность и единичные старшие биты. В этом случае считается, что вычитаемое больше вычитаемого, что влечет за собой включение 1 в частное и выполнение операции CRC-вычитания. Это как раз и есть проявление слабого понятия размерности. Корзина для мусора, показанная на рис. 9.4, означает тот факт, что частное для процесса вычисления CRC-битовой последовательности не имеет никакого значения.
Реальные двоичные последовательности являются результатом сцепления порой огромного количества отдельных байтов (символов), образуя одно большое двоичное число, для представления которого нужно использовать двоичные полиномы огромных степеней. При этом каждый бит в подобной последовательности произвольной длины представляется в виде коэффициента длинного полинома.
Например, для представления 128-разрядного блока необходим полином, состоящий из 1024 слагаемых, а для 1024-битного блока необходим полином уже с 8192 слагаемыми. В терминах полиномиальной арифметики двоичное число, сформированное в результате подобной сцепки составляющих блока данных, называется полиномом данных {сообщения) и обозначается как D(x).
В алгоритме вычисления CRC вводится еще несколько полиномов и соотношений между ними:
- порождающий полипом G(x) – предварительно особым образом выбранный полином, на который делится исходный полином сообщения;
- полином-частное Q(x) – полином, получившийся в качестве частного от деления полиномов D(x)/G(x);
- полином-остаток R(x) – полином, получившийся в качестве остатка от деления полиномов D(x)/G(x).
