Прямой алгоритм вычисления CRC
Описанный выше алгоритм вычисления значения CRC называется прямым и чаще всего реализуется аппаратно. Но, тем не менее, для совершенствования навыков программирования на ассемблере составим реализующий его пример программы. Хотя эффективность этой программы не слишком высока, у нее есть две учебные цели:
- показать в виде программной реализации суть алгоритма вычисления CRC и самого CRC-деления;
- подготовить себя к пониманию более совершенных алгоритмов расчета CRC, к которым относится, в частности, рассматриваемый ниже табличный алгоритм.
Для компьютерной реализации алгоритмов вычисления CRC удобно выбирать полиномы со степенями, кратными 8 (то есть размерности регистров) – 8, 16, 24, 32 или даже 64. В этом случае можно подобрать команды из системы команд микропроцессора, наиболее оптимально реализующие алгоритмы вычисления CRC. В качестве полинома выберем один из рекомендуемых полиномов (см. ниже) – 4003. И еще одно важное замечание – степень полинома определяет размерность регистра, используемого в алгоритме, при этом считается, что старший (всегда единичный) бит полинома находится сразу за левой границей регистра. В этих условиях программа реализации прямого алгоритма вычисления CRC функционирует следующим образом (для лучшего понимания в процессе разбора алгоритма см. рис. 9.6). В регистр побитно вдвигаются биты исходной строки.
Это происходит до тех пор, пока при очередном сдвиге слева появится единичный бит. В этом случае все содержимое регистра подвергается операции XOR со значением полинома без старшего бита. Далее процесс сдвига и анализа выдвигаемого бита продолжается до тех пор, пока не будет выдвинут очередной единичный бит, в результате чего опять между регистром и полиномом выполняется операция XOR, и т. д. После того как последний бит вдвинут в регистр, в него вдвигается количество нулевых битов, равное степени полинома. Этим, как мы не раз уже отмечали, достигается участие всех бит исходной битовой строки в формировании значения CRC. В результате в регистре остается значение CRC, которое необходимо добавить к исходной строке и передать приемнику.
jnc m5;старшие разряды не равны – выполняем сдвиг (частное нас не интересует) ;старшие разряды равны – выполняем XOR: хог eax.ebx;eax(31..16) XOR pollnom т5: loop m4
В результате вычисления CRC символьной последовательности "6476с8" получим CRC 35dah.
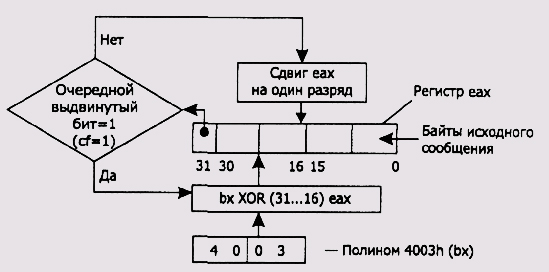
Рис. 9.6. Схема вычисления значения CRC прямым алгоритмом
Для того чтобы смоделировать действия стороны приемника, можно использовать ту же самую программу со слегка измененными исходными данными – к строке bitstring добавляем вычисленное значение CRC. После этого под отладчиком наблюдаем за процессом CRC-деления, причем контролируем остаток от деления. В определенный момент увидим, что он стал нулевым – это свидетельствует о том, что исходная последовательность не была изменена. Для эксперимента можно изменить значения одного или более битов исходной последовательности и посмотреть, что получится.
;prg09_02.asm – программа демонстрации прямого алгоритма вычисления CRC;(сторона-приемник). .data ;исходная битовая последовательность в символах bit_string db "6476c8",35h.0dah len_bit_stri ng=$-bi t_stri ng adr_bit_string dd bit_string polinomdw 4003h .code main: :см. предыдущую программу exit::выход из программы
Очевидный недостаток прямого метода – большое количество операций сдвига, исключающих операций ИЛИ (XOR) и операций условного перехода, которые выполняются для каждого бита исходного сообщения. Поэтому на практике используется другой способ расчета CRC, называемый табличным.