Цифровые сигнатуры (подписи)
Если сборка должна быть развернута в глобальном кэше сборок, то необходимо, чтобы она имела цифровую подпись. Цифровая подпись (сигнатура) не требуется и не особенно полезна для сборки, развернутой частным образом, так как частная сборка развертывается пользователем для того, чтобы работать со своей определенной клиентской программой и потому согласована с ней. Если даже развернутая частным образом сборка имеет цифровую подпись, общеязыковая среда выполнения CLR по умолчанию не проверяет этого, когда загружает сборку для клиентской программы. Поэтому ответственность за предотвращение неправомочной модификации или подтасовки развернутых частным образом сборок полностью возложена на администратора. С другой стороны, очень выгодно использовать общедоступно развернутые (т.е. общедоступные) сборки, так как они должны быть подписаны в цифровой форме, и потому обычно их используют многие клиенты, причем рядом могут существовать несколько версий одной сборки.
Цифровые подписи (сигнатуры) основаны на криптографических методах, в которых применяются открытые ключи. В мире криптографии применяется два основных криптографических метода – симметричные шифры (общий ключ) и асимметричные шифры (открытый ключ). Симметричные шифры совместно используют секретный ключ как для кодирования, так и для расшифровки. Стандарт шифрования данных DES (Data Encryption Standard), Triple DES (Тройной стандарт шифрования данных) и RC2 – примеры симметричных алгоритмов шифрования.
Симметричные шифры могут быть очень эффективными и мощными в обеспечении секретности сообщения между двумя доверяющими друг другу сотрудничающими лицами, но они не совсем подходят для ситуаций, где трудно совместно использовать секретный ключ. По этой причине симметричные шифры считаются неподходящими для цифровых подписей (сигнатур). Именно потому цифровые подписи (сигнатуры) используются не для секретности, а лишь для идентификации и опознавания, что является более открытым делом. Если бы вы совместно использовали ваш симметричный ключ с каждым, кто потенциально хотел бы убедиться в подлинности ваших сборок, то по неосторожности могли доверить его людям, которым захотелось исполнить вашу роль. Для использования в цифровых подписях (сигнатурах) намного лучше подходят асимметричные шифры.
Асимметричные шифры, которые также называются шифрами с открытым ключом, используют криптографическую пару открытого и секретного ключа. Ключи в паре математически связаны, и генерируются они вместе; однако чрезвычайно трудно вычислить один ключ по другому. Обычно открытый ключ выдается каждому, кто хотел бы убедиться в подлинности владельца сборки С другой стороны, владелец сохраняет соответствующий секретный ключ подписи в тайне, чтобы никто не мог подделать его подпись. Метод шифрования по схеме открытого ключа RSA (RSA-кодирование) – пример системы шифрования с открытым ключом.
Шифрование с открытым ключом основано на очень интересной математической схеме, которая позволяет зашифровать обычный текст одним ключом, а расшифровать, только зная ключ, соответствующий исходному Например, когда открытый ключ используется, чтобы зашифровать первоначальные данные (называемые открытым текстом), только соответствующий секретный ключ может помочь в расшифровке этого текста. Даже ключ, который использовался для шифрования, не поможет в расшифровке зашифрованного текста! Этот сценарий полезен тогда, когда секретные сообщения посылаются только человеку, который знает секретный ключ.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Рассмотрим теперь противоположный сценарий. Человек, который знает секретный ключ, использует его для того, чтобы зашифровать открытый текст. Получающийся зашифрованный текст не является тайной, так как каждый заинтересованный может получить открытый ключ, чтобы расшифровать данный текст. Этот сценарий бесполезен для сохранения тайны, но очень эффективен для опознавательных целей. Нет необходимости шифровать исходные данные полностью, поэтому, чтобы повысить эффективность, вместо них шифруется компактный хэш-код, который с высокой вероятностью характерен для исходных данных.
Если вы получаете файл, который содержит зашифрованную версию его собственного хэш-кода, и расшифровываете его с помощью соответствующего открытого ключа, то фактически вы повторно вычислите хэш-код исходных данных. И если теперь вы обнаружите, что он совпадает с хэш-кодом, который был зашифрован, можете быть совершенно уверены, что именно владелец секретного ключа приложил цифровую подпись и данные не были изменены другими лицами Если предположить, что владелец сумел сохранить тайну секретного ключа, тогда совпадение результатов вычисления доказывает, что никто не смог бы исказить файл после того, как он был подписан в цифровой форме. На рис. 7.3 показано, как работает цифровая подпись (сигнатура).
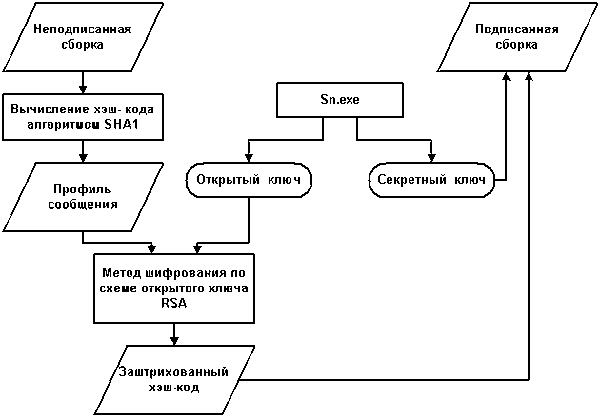
Рис. 7.3. Вот так работает цифровая подпись (сигнатура)
Цифровое подписание методом шифрования по схеме открытого ключа RSA и SHA1
Чтобы подписать сборку, производитель вычисляет с помощью алгоритма SHA1 ее хэш-код (причем байты, зарезервированные для подписи (сигнатуры), предварительно обнуляются), и затем зашифровывает значение хэш-функции с помощью секретного ключа, используя метод шифрования по схеме открытого ключа RSA (RSA-кодирование). Открытый ключ и зашифрованный хэш-код сохраняются в метаданных сборки.
