Ранжированные переменные и таблицы вывода
Задание ранжированных переменных
Ранжированные переменные – особый класс переменных, который в системе MathCAD зачастую заменяет управляющие структуры, называемые циклами (однако полноценной такая замена не является). Эти переменные имеют ряд фиксированных значений (либо целочисленных, либо в виде чисел), с определенным шагом меняющихся от начального значения до конечного.
Ранжированные переменные характеризуются именем и индексом каждого своего элемента. Для создания ранжированной переменной целочисленного типа используется выражение:
Name Nbegin Nend
…где Name – имя переменной, Nbegin – ее начальное значение, Nend – конечное значение, – символ, указывающий на изменение переменной в заданных пределах (он вводится знаком точки с запятой,). Если Nbegin < Nend, то шаг изменения переменной будет равен +1, в противном случае -1.
Для создания ранжированной переменной общего вида используется выражение:
Name = Nbegin, (Nbegin+ Step) Nend
Здесь Step – заданный шаг изменения переменной (он может быть положительным, если Nbegin < Nend или отрицательным в противном случае).
Таблицы вывода
Ранжированные переменные широко применяются для представления числовых значений функций в виде таблиц, а также для построения их графиков. Любое выражение с ранжированными переменными после знака равенства инициирует таблицу вывода. Несколько таких таблиц показано на рис. 11.3.
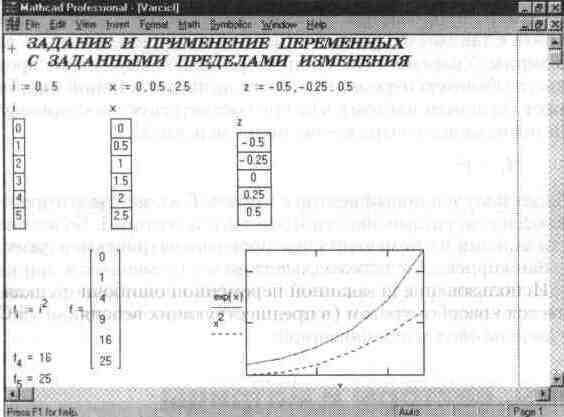
Рис. 11.3. Примеры типового применения ранжированных переменных
Полезно учитывать некоторые свойства таблиц вывода:
- число строк в них не может быть больше 50 (большие таблицы придется составлять из нескольких малых);
- числа в таблицах можно задавать в требуемом формате с помощью операций задания формата чисел;
- при использовании в таблице единиц размерности все данные таблицы будут содержать единицы размерности (поделите результат с размерными переменными на размерность для указания ее только в заголовке таблицы вывода);
Есть три способа показать значения векторов:
- Х,= выводится обычная таблица вывода;
- Х= выводится вектор, если число его элементов меньше 10;
- Х= выводится таблица вывода со слайдером, если число элементов вектора больше 10.
В таблицы вывода можно и вставлять числовые значения, и корректировать их. Естественно, это меняет значения элементов соответствующего вектора.
Применение ранжированных переменных
Важно отметить, что в сущности задание ранжированных переменных эквивалентно заданию конечных циклов. Сами ранжированные переменные являются векторами, что видно из выдачи их значений (столбец со всеми значениями переменных). Это означает, что объем памяти, занимаемый такими переменными, больше занимаемого обычными переменными.
Индексированные переменные, образующиеся в результате задания ранжированных переменных, могут применяться в последующих фор-мульных блоках. Однако в этих блоках необходимо соблюдать соответствие результатов (конечных и промежуточных) векторному типу этих переменных.
Привыкшие к обычному программированию пользователи часто забывают, что ранжированная переменная – вектор. Поэтому они пытаются выполнять с такими операциями действия, корректные лишь для обычных (скалярных) переменных. Например, задают выражение вроде f:=i*2, используя обычную переменную f, что приведет к явной ошибке – система укажет (красным цветом), что f не соответствует векторному типу. Однако если использовать выражение, например, вида:
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
f,:= i^2
…то будет получен новый вектор с именем f, элементы которого в нашем случае являются квадратами значений элементов вектора i. Более подробно особенности задания и применения векторов рассматриваются далее.
Ранжированные переменные широко применяются при построении графиков. Например, для построения графика некоторой функции f(x) прежде всего надо позаботиться о создании ряда значений переменной х, для этого она должна быть ранжированной.
