Директивы моделирования
Monte Carlo/Worst Case – статистический анализ и наихудший случай
Статистический анализ по методу Монте-Карло (Monte Carlo) производится при статистическом разбросе параметров, описанных по директиве .MODEL. Случайное значение параметра х рассчитывается по формуле где x HOM – номинальное значение параметра, указанное в директиве .MODEL; А – относительный разброс параметра х; £, – центрированная случайная величина, принимающая значения на отрезке (-1, +1).
Случайные величины создаются с помощью генераторов случайных чисел. Величина относительного разброса каждого параметра А и закон распределения случайной величины £, задаются опцией <спецификация случайного разброса параметра> директивы .MODEL, которая имеет вид:
[DEV[/<генератор#>] [/ <закон распределения>] <разброс>[%]] [LOT[/<генератор#>] [/<закон распределения>] <разброс>[%]}Параметр <генератор #> указывает номер генератора случайных чисел (от О до 9). С его помощью создаются коррелированные параметры. Случайные параметры, для которых не указаны номера генераторов случайных чисел, образуются с помощью индивидуальных независимых генераторов; они, естественно, являются некоррелированными. Для расчета значений разбросов параметров DEV и LOT используются различные генераторы: имеется 10 генераторов для параметров DEV и столько же для параметров LOT.
В простейшем случае номера генераторов случайных чисел не указываются. Тогда параметры, имеющие опции DEV, получают независимые, а параметры, имеющие опции LOT, – коррелированные случайные значения (последнее характерно для имитации разброса параметров партий изделий).
Приведем примеры:
.MODEL RLOAD RES (R=1 DEV/GAUSS 5% LOT/UNIFORM 10%) .MODEL CMOD CAP (C=1 DEV/4/GAUSS 1% TC1 DEV/4/USER1 10% LOT/5 2%)В программе имеются генераторы случайных величин с двумя стандартными законами распределения:
- UNIFORM – равновероятное распределение на отрезке (-1, +1);
- GAUSS – гауссовское распределение на отрезке (-1, +1) с нулевым средним значением и среднеквадратическим отклонением ст = 0.25 (т.е. создается усеченное гауссовское распределение на интервале ±4а).
Кроме того, пользователь может задать нестандартный закон распределения случайных величин £, с помощью директивы:
.DISTRIBUTION <имя> <<^><P>>;*Здесь параметр <имя> назначает имя закону распределения, который задается в табличной форме. Пары чисел задают значения случайной величины % и соответствующую вероятность Р. Всего может быть задано до 100 точек. Все значения % должны находиться на интервале (-1, +1). Координаты точек должны указываться в порядке возрастания £, (допускается повторять предыдущие значения £). Между соседними точками производится линейная интерполяция. Приведем пример задания бимодального распределения, график которого изображен на рис. 4.8:
.DISTRIBUTION BI_MODAL (-1.1) (-5.1) (-0.5.0) (.5.0) (.5.1) (1.1)Случайным параметрам, закон распределения которых не задан явно в директиве .MODEL, по умолчанию назначается распределение, указанное в опции DISTRIBUTION директивы .OPTIONS. Статистические испытания по методу Монте-Карло проводятся при расчете режима по постоянному току, переходных процессов или частотных характеристик по директиве:
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
.MC <n> [DC] [IRAN] [AC] <имя выходной переменой>+ <обработка результатов> [LIST] + [OUTPUT <спецификация>] [NAME(<минимум>,<максимум>)] + [SEED=<значение>]Параметр <п> задает количество статистических испытаний. Ключевые слова DC, TRAN, АС указывают вид анализа. После них указывается <имя выходной переменной>, подлежащей статистической обработке.
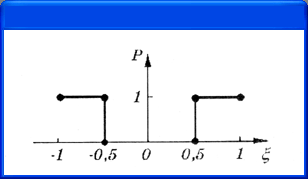
Рис. 4.4. Бимодальный закон распределения
