Иллюстрированный самоучитель по Web-графике

О сжатии информации

Существует еще один алгоритм сжатия – Шеннона-Фано, основанный на тех же идеях, но не гарантирующий максимального сжатия, как алгоритм Хаффмена. Код Шеннона-Фано строится с помощью дерева. Однако построение этого дерева начинается от корня. Все множество кодируемых элементов соответствует корню дерева (вершине первого уровня). Оно разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Эти подмножества соответствуют двум вершинам второго уровня, которые соединяются с корнем. Далее каждое из этих подмножеств разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Им соответствуют вершины третьего уровня. Если подмножество содержит единственный элемент, то ему соответствует концевая вершина кодового дерева; такое подмножество разбиению не подлежит. Подобным образом поступаем до тех пор, пока не получим все концевые вершины. Ветви кодового дерева размечаем символами 1 и 0, как в случае кода Хаффмена.

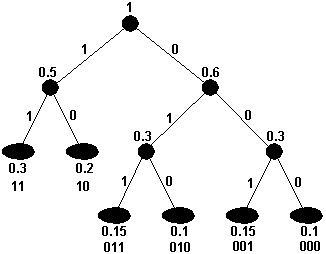
Рис. 99. Кодовое дерево Шеннона-Фано

При построении кода Шеннона-Фано разбиение множества элементов может быть произведено, вообще говоря, несколькими способами. Выбор разбиения на уровне n может ухудшить варианты разбиения на следующем уровне (n+1) и привести к неоптимальности кода в целом. Другими словами, оптимальное поведение на каждом шаге пути еше не гарантирует оптимальности всей совокупности действий. Поэтому код Шеннона-Фано не является оптимальным в общем смысле, хотя и дает оптимальные результаты при некоторых распределениях вероятностей. Для одного и того же распределения вероятностей можно построить, вообще говоря, несколько кодов Шеннона-Фано, и все они могут дать различные результаты. Если построить все возможные коды Шеннона-Фано для данного распределения вероятностей, то среди них будут находиться и все коды Хаффмена, т. е. оптимальные коды.

Каковы распределения частот встречаемости элементов в реальных изображениях? Может показаться, что они могут быть самыми разными. Однако у них есть нечто общее.

Известно, что буквы алфавита имеют различные частоты встречаемости в текстах. При этом в достаточно больших по объему текстах эти частоты остаются практически неизменными. В свое время Ципф заинтересовался частотами встречаемости слов (точнее говоря, словоформ) и обнаружил интересную зависимость. Так, если все слова в тексте расположить в порядке убывания частот их встречаемости и пронумеровать, то частота р_i i-гo слова будет приблизительно обратно пропорциональна его номеру i, т. е. выполняется зависимость р_i ~ 1/i. Характер этой зависимости таков, что в тексте можно выделить относительно небольшую группу очень часто встречающихся слов и много слов, которые редко встречаются. Дальнейшие исследования показали, что эта зависимость, получившая название "закона Ципфа", выполняется не только для текстов, но и для графических изображений и даже музыки. Если говорить о графике, то поступали следующим образом. Брали лист бумаги с картинкой и разрезали его на кусочки так, чтобы каждый кусочек имел приблизительно только один цвет. Затем эти кусочки сортировали по цвету и взвешивали. Относительные массы таких групп кусочков можно считать частотами встречаемости соответствующих цветов в исходном изображении. Позднее Б. Мандельброт уточнил формулу Ципфа, введя в нее дополнительные параметры (новую формулу назвали законом Ципфа-Мандельброта). Это позволило приблизить данную зависимость к реально наблюдаемым данным.

Оказалось, что если закон Ципфа хорошо выполняется на некотором объекте (тексте, картинке), то на произвольно выбранных частях этого объекта он уже не будет выполняться. Кроме того, выяснилось, что чем лучше объект соответствует нашим интуитивным представлениям о гармонии, системном единстве и т. п., тем ближе реально наблюдаемая зависимость р_i (i) к закону Ципфа, и наоборот. Именно это обстоятельство легло в основу гипотезы о том, что закон Ципфа выполняется на хорошо организованных объектах. Более глубокие исследования показали, что закон Ципфа можно объяснить тем, что, создавая художественное произведение, человек интуитивно стремится к оптимальному (с точки зрения кодирования) представлению информации. Распределение частот встречаемоcти, описываемое формулой Ципфа-Мандельброта, очень подходит для того, чтобы кодирование (сжатие) с помощью алгоритмов Хаффмена и Шеннона-Фано давало высокую степень сжатия. Следует заметить, что существуют тексты и графические изображения, для которых распределения частот элементов весьма далеки от описываемых формулой Ципфа-Мандельброта.

Другой подход к задаче сжатия данных основан на кодировании блоков пикселов и словарях или таблицах поиска данных. Одним из простейших методов этого типа является RLE (Run Length Encoding, кодирование с переменной длиной). Метод RLE заключается в поиске блоков из одинаковых пикселов, находящихся в одной строке прямоугольной картинки. Затем каждому блоку сопоставляется число содержащихся в нем пикселов и цвет. Например, если в строке имеются 3 пиксела белого цвета, 25 – черного, затем 14 – белого, то применение RLE кодирует эту строку как 3 белых, 25 черных и 14 белых вместо последовательности из кодов цветов всех 42 пикселов. Метод RLE используется, например, при создании файлов формата BMP.

Метод сжатия LZW (Lempel-Ziv-Welch) разработан в 1978 году. Он заключается в поиске одинаковых последовательностей (фраз) пикселов во всем файле. Выявленные последовательности сохраняются в таблице, им присваиваются более короткие коды (ключи). Так, если в изображении имеются наборы из красного, желтого и зеленого пикселов, повторяющиеся в изображении, например, 50 раз, то алгоритм LZW выявляет это, присваивает данному набору пикселов отдельный код (число), а затем сохраняет этот код 50 раз. Метод LZW так же, как и RLE, лучше работает на участках однородных, свободных от шума цветов. Он дает гораздо лучшие результаты, чем RLE, при сжатии произвольных графических данных, но процессы кодирования и распаковки происходят медленнее. Метод LZW используется, например, при создании файлов формата GIF.