О сжатии информации
Прежде чем перейти собственно к графическим форматам, рассмотрим принципы сжатия данных. Сжатие (компрессия) имеет очень большое значение при создании файлов с мультимедийной информацией. Без него файлы имели бы неприемлемо большой объем.
Алгоритмы сжатия, используемые при создании файлов, делятся на два класса: обеспечивающие сжатие без потери информации и допускающие некоторую ее потерю. Сжатие без потерь основано на удалении избыточности исходного представления информации, т. е. на применении более экономного кодирования. Такое сжатие еще называют обратимым. Сжатие с потерями базируется на удалении некоторой части информации. В ряде случаев эти потери оказываются практически незаметными для зрения или вполне допустимыми. Это относится главным образом к изображениям типа фотографии. Опыт показывает, что довольно часто за счет незначительной потери качества такого изображения можно существенно сократить объем файла. Сжатие с потерями называют также необратимым.
Рассмотрим основные идеи алгоритмов сжатия данных без потерь. Но сначала приведем простой пример. Допустим, исходная информация представлена в виде следующей последовательности букв:
ААААББВВВАААААААСамо собой напрашивается более экономное представление этой информации: А4Б2ВЗА7. Здесь число указывает количество повторений буквы, указанной слева от числа. Алгоритм декодирования этой последовательности очевиден: каждую букву необходимо записать столько раз, сколько указано числом справа от нее. В данном случае мы сократили объем данных в 2 раза, причем без потерь, поскольку есть декодирующий алгоритм, полностью восстанавливающий исходные данные. Коль скоро нам это удалось, то можно сказать, что исходное представление информации было избыточным. Многие изображения (например, темные линии на белом фоне) содержат большие области одинаковых пикселов. Каждому пикселу соответствует одно число (яркость в оттенках серого или индекс) или несколько чисел (обычно три, по количеству базовых цветов). Для таких картинок описанный выше алгоритм сжатия обычно дает хорошие результаты. Если говорить более общо, то исходное представление информации можно рассматривать как последовательность битов (нулей и единиц) или байтов (блоков из восьми битов). А раз так, то не принципиально, что собственно содержит исходная запись: текст, программу или графическое изображение. Алгоритмы сжатия могут быть универсальны. Однако они могут иметь различную сложность (быстродействие) и обеспечивать разную степень сжатия. Для любого алгоритма можно найти набор данных, для которого этот алгоритм окажется не хуже других. С другой стороны, существуют такие наборы данных, которые не сжимаются никаким алгоритмом. Так, любой набор случайных данных с равномерным законом распределения вероятностей их появления не сжимается. Наличие же каких-то регулярностей (повторений, зависимостей) в исходных данных обеспечивает возможность их более экономного представления, т. е. сжатия.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Простейшие алгоритмы сжатия, называемые также алгоритмами оптимального кодирования, основаны на учете распределения вероятностей элементов исходного сообщения (текста, изображения, файла). На практике обычно в качестве приближения к вероятностям используют частоты встречаемости элементов в исходном сообщении. Вероятность – абстрактное математическое понятие, связанное с бесконечными экспериментальными выборками данных, а частота встречаемости – величина, которую можно вычислить для конечных множеств данных. При достаточно большом количестве элементов в множестве экспериментальных данных можно говорить, что частота встречаемости элемента близка (с некоторой точностью) к его вероятности.
Если вероятности неодинаковы, то имеется возможность наиболее вероятным (часто встречающимся) элементам сопоставить более короткие кодовые слова и, наоборот, маловероятным элементам сопоставить более длинные кодовые слова. Таким способом можно уменьшить среднюю длину кодового слова. Оптимальный алгоритм кодирования делает это так, чтобы средняя длина кодового слова была минимальной, т. е. при меньшей длине кодирование станет необратимым. Такой алгоритм существует, он был разработан Хаффменом и носит его имя. Этот алгоритм используется, например, при создании файлов в формате JPEG.
Суть алгоритма Хаффмена удобно объяснить через построение кодового дерева – графа древовидной формы. Дерево строится от концевых вершин по направлению к корню, снизу вверх. Сначала упорядочим все элементы сообщения по невозрастанию или по неубыванию (это не принципиально) их вероятностей (частот встречаемости). Эти элементы образуют концевые вершины дерева, называемые также листьями. Выберем две из них с наименьшими вероятностями. Построим новую вершину, из которой одна ветвь идет к одному элементу, а другая – к другому. Этой новой вершине припишем вероятность, равную сумме вероятностей вершин, с которыми она соединена. Далее рассмотрим все оставшиеся концевые вершины и только что построенную. Выберем из них две с минимальными вероятностями и соединим их с новой вершиной, которой припишем сумму вероятностей объединяемых вершин. Поступаем так до тех пор, пока не останется ни одной пары вершин, которые можно было бы объединить. В результате получится дерево. Очевидно, что вероятность, приписанная корню дерева, равна 1. Теперь разметим ветви, выходящие из вершин: одной из них припишем 1, а другой 0, если хотим получить кодовые слова в таком алфавите. Сделаем это для всех пар ветвей. Тогда последовательность нулей и единиц, которую можно собрать, двигаясь от корня дерева к концевой вершине, образует кодовое слово для соответствующего элемента.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
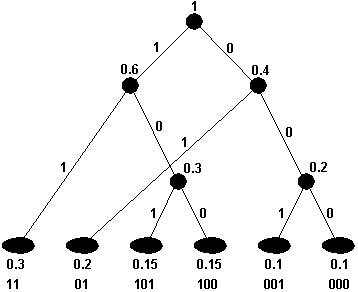
Рис. 98. Кодовое дерево Хаффмена
Средняя длина кодового слова вычисляется как взвешенная вероятностями сумма длин всех кодовых слов:
Lcp = p1L1 + p2L2 +… + pnLn
Где p1,…, pn – вероятности кодовых слов;
L1,…, Ln – длины кодовых слов.
Клод Шеннон в 40-х годах XX века в своей "Математической теории связи" показал, что средняя длина кодового слова не может быть меньше, чем энтропия множества кодируемых элементов, которая вычисляется по формуле:
Н = p1log(1/p1) + p2log(l/p2) +… + pnlog(l/ pn)
Средняя длина кодового слова, обеспечиваемая кодом Хаффмена, приближается к энтропии при очень больших объемах сообщений. При этом длина кодового слова, имеющего вероятность р, приближается к log (l/p). В случае кодирования двоичными символами основание логарифмов в приведенных выше формулах равно 2.
Если не учитывать вероятности (т. е. считать их равными), то для кодирования n элементов с помощью нулей и единиц потребуется log(n) битов на каждый элемент. Точнее говоря, в качестве длины слова следует взять ближайшее большее целое для этого числа. Так, например, для кодирования 6 элементов потребуются слова длиной 3 (log(6) = 2.585). При этом все слова будут иметь одинаковую длину. Если же учесть вероятности, то для рассмотренного выше примера средняя длина кодового слова будет равна 2.5 (0.5x2 + 0.5x3). При кодировании достаточно больших сообщений это дает экономию около 17%.
Код Хаффмена реализует обратимое и максимальное сжатие данных (обратимость означает, что имеется возможность полного восстановления исходного сообщения). Максимальность сжатия понимается в следующем смысле. Если источник сообщений генерирует символы с фиксированным распределением вероятностей, то при кодировании сообщений, длина которых стремится к бесконечности, достигается средняя длина кодового слова, равная энтропии. Следует заметить, что для одного и того же распределения вероятностей можно построить, вообще говоря, несколько кодов Хаффмена, но все они дают одинаковые результаты.
