Введение в конечные автоматы
Применительно к драйверам внешних устройств, циклический граф может соответствовать повторным попыткам выполнения операции после ее не-'удачи. Понятно, что на практике количество таких попыток следует ограничивать. Самый простой способ такого ограничения – введение счетчика попыток. Формально после этого состояния с различными значениями счетчика превращаются в наборы состояний, а граф переходов становится ациклическим (рис. 10.6), но для достаточно большого количества повторений опять-таки необозримым, поэтому на практике часто используют сокращенную блок-схему, в которой состояния с разными значениями счетчика цикла изображаются как одно состояние.
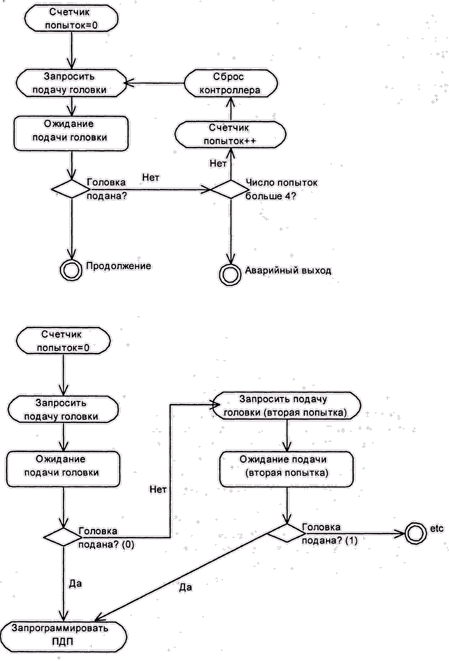
Рис. 10.6. Развертывание циклов в графе состояния
Анализ полной или сокращенной блок-схемы алгоритма методами теории графов, хотя и не может однозначно дать ответ на вопрос о его финитности, может оказать значительную помощь в оценке алгоритма, в том числе и в поиске "узких" с точки зрения финитности мест. В [Кнут 2000) приводятся примеры такого анализа для некоторых простых алгоритмов.
Алгоритмы основной массы реально применяемых программ (особенно использующих переменные состояния большого объема) имеют совершенно Необозримые блок-схемы. Отчасти это обходится декомпозицией программного комплекса на отдельные модули с более обозримой функциональностью и алгоритмом, но все-таки далеко не для всех алгоритмов представление в виде конечного автомата естественно.
С другой стороны, ряд даже довольно сложных алгоритмов естественным образом описывается автоматами с небольшим числом состояний, которые могут быть закодированы одной скалярной переменной состояния или стеком таких переменных. Такие автоматы находят применение в самых разнообразных задачах: лексическом и синтаксическом разборе контекстно-свободных и многих типах контекстно-связанных языков [Кормен/ Пейзерсон/Ривест 2000 1, реализации сетевых протоколов, задачах корпоративного документооборота (Керн/Линд 2000] и др. В частности, легко понять, что обсуждаемый нами алгоритм драйвера относится именно к этой категории алгоритмов.
Два основных подхода к реализации конечных автоматов – это развернутые (unrolled) автоматы и автоматы общего вида. Примером развернутого конечного автомата является код основной нити примера 10.2. Понятно, что развертыванию поддаются только автоматы с весьма специфической – линейной или древовидной – структурой графа состояний, и если в процессе уточнения требований мы выясним, что структура автомата должна быт более сложной, нам придется полностью реорганизовать код.
Автомат общего вида выглядит несколько сложнее, но, научившись распознавать его конструкцию, легко разрабатывать такие программы по задан ной блок-схеме и, наоборот, восстанавливать граф состояний по коду программы. Главным преимуществом грамотно реализованного конечного автомата является легкость модификации: если граф переходов измените нам надо будет изменить код только тех узлов, которые затронуты изменением.
