Введение в конечные автоматы
Конечный автомат (в современной англоязычной литературе используется также более выразительное, на взгляд автора, обозначение, не имеющее хорошего русского эквивалента – state machine, дословно переводимое как машина состояний) представляет собой устройство, имеющее внутреннюю память (переменные состояния), а также набор входов и выходов. Объем внутренней памяти у конечных автоматов, как следует из названия, конечен. Автоматы с неограниченным объемом внутренней памяти называются бесконечными автоматами, нереализуемы и используются только в теоретических Построениях [Минский 1971].
Однако некоторые разновидности теоретически бесконечных автоматов – например, стековые – могут быть реализованы в форме автоматов с практически неограниченной памятью – например, достаточно глубоким стеком – и находят практическое применение, например при синтаксическом анализе языков со вложенными структурами [Кормен/Лейзерсон/Ривест 2000].
Работа автомата состоит в том, что он анализирует состояния своих входов, и, в зависимости от значений входов и своего внутреннего состояния, изменяет значения выходов и внутреннее состояние. Правила, в соответствии с которыми происходит изменение, описываются таблицей или диаграммой переходов. Диаграмма переходов представляет собой граф, вершины которого соответствуют допустимым состояниям внутренних переменных автомата, а ребра – допустимым переходам между ними. Переходы между вершинами направленные: наличие перехода из А в В не означает, что существует переход из В в А. Наличие перехода в обоих направлениях символизируется двумя ребрами, соединяющими одну пару вершин. Такой граф называется ориентированным [Кормен/Лейзерсон/Ривест 2000]. Таблица переходов может рассматриваться как матричное представление диаграммы переходов.
Блок-схемы (рис. 10.5) являются обычным способом визуализации графов переходов и используются для описания алгоритмов с 60-х годов. Любой алгоритм, исполняющийся на фон-неймановском компьютере с конечным объемом памяти (а также любой физически исполнимый алгоритм), может быть описан как конечный автомат и изображен в виде блок-схемы.
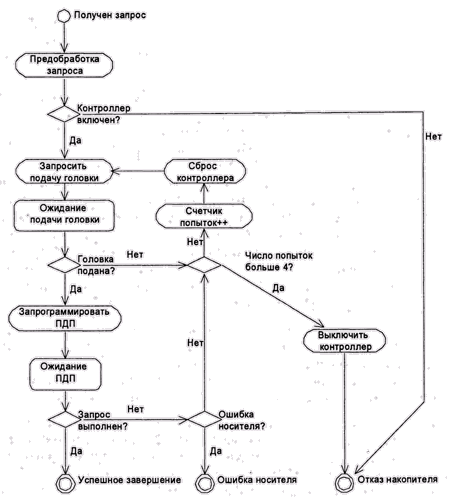
Рис. 10.5. Блок-схема драйвера
У конечных автоматов с ограниченным числом допустимых значений входов, граф переходов всегда конечен, хотя и может содержать циклы (замкнутые пути) и контуры (совокупности различных путей, приводящих к одной и той же вершине). Понятно, что для автомата с графом, содержащим циклы, невозможно гарантировать финитности – завершения работы за конечное время. Как известно, задача доказательства финитности алгоритма, хотя и решена во многих частных случаях, в общем случае алгоритмически неразрешима [Минский 1971].
