Иллюстрированный самоучитель по созданию чертежей

Сопряжение дуг окружностей прямой линией. Сопряжение двух дуг окружностей третьей дугой.

При построении сопряжения дуг окружностей прямой линией можно рассмотреть две задачи: сопрягаемая прямая имеет внешнее или внутреннее касание. В первой задаче (рис. 33, а) из центра дуги меньшего радиуса R1 проводят касательную вспомогательной окружности, проведенной радиусом R – RI. Ее точку касания Ко используют для построения точки сопряжения А на дуге радиуса R.

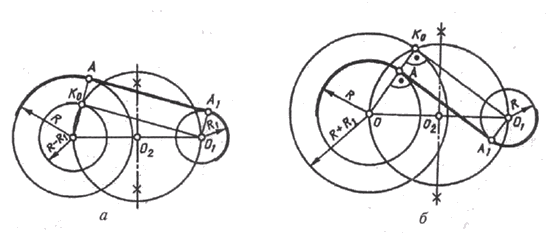
Рис. 33

Для получения второй точки сопряжения А₁ на дуге радиуса R₁ проводят вспомогательную линию О₁ А₁ параллельно О А. Точками A и А₁ будет ограничен участок внешней касательной прямой.

Задача построения внутренней касательной прямой (рис. 33, б) решается, если вспомогательную окружность построить радиусом, равным R + R₁.

Сопряжение двух дуг окружностей третьей дугой

При построении сопряжения двух дуг окружностей третьей дугой заданного радиуса можно рассмотреть три случая: когда сопрягающая дуга радиуса R касается заданных дуг радиусов R₁ и R₂ с внешней стороны (рис. 34, а); когда она создает внутреннее касание (рис. 34, б); когда сочетаются внутреннее и внешнее касания (рис. 34, в).

Построение центра О сопрягающей дуги радиуса R при внешнем касании осуществляется в следующем порядке: из центра О₁ радиусом, равным R + R₁, проводят вспомогательную дугу, а из центра O₂ проводят вспомогательную дугу радиусом R + R₂. На пересечении дуг получают центр О сопрягаемой дуги радиуса R, а на пересечении радиусом R + R₁ и R + R₂ с дугами окружностей получают точки сопряжения А и А₁.

Построение центра О при внутреннем касании отличается тем, что из центра О₁ проводят вспомогательную окружность радиусом, равным R – R₁ а из центра О₂ радиусом R – R₂. При сочетании внутреннего и внешнего касания из центра О₁ проводят вспомогательную окружность радиусом, равным R – R₁, а из центра О₂ – радиусом, равным R + R₂.