Зависимые источники сигналов
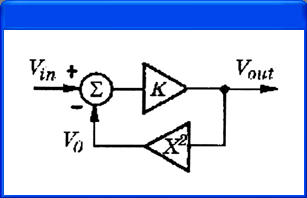
Рис. 4.18, а) Моделирование функциональных схем: а – устройство вычисления квадратного корня; б – эквивалентная принципиальная схема для PSpice
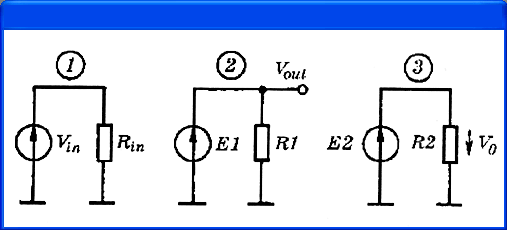
Рис. 4.18, б)
Замечание
Отметим, что наличие в схемном редакторе PSpice Schematics библиотеки символов функциональных блоков amb.slb позволяет не составлять электрические схемы замещения функциональных схем типа рис. 4.18, б, а сразу составлять функциональные схемы из имеющихся стандартных функциональных блоков (см. Приложение 1 [7]).
Продемонстрируем методику решения дифференциальных уравнений на примере системы уравнений:
- dx 1 /dt=-0.3 x l +x 2 +x 1 2 -3х 1 х 2 -x 1
- dx 2 /dt= 0.24-0.6x 2 + 4x 1 x 2 – 6x 1 2 x 2 at
…с начальными условиями х 1 (0) = 0, х 2 (0) = 0.4. Используя уравнение конденсатора i = Cdu/dt, смоделируем систему дифференциальных уравнений с помощью зависимых источников тока GX1, GX2, подключенных к конденсаторам C1, C2, как показано на рис. 4.19. На входном языке программы PSpice задание на моделирование составляется следующим образом:
DIFFERENTIAL EQUATIONS GX1 0 1 POLY(3) (1.0) (2.0) (0.0) 0-0.3 101-300001GX2 0 2 POLY(3) (1.0) (2.0) (0.0) 0.6 0-0.6 00400000-6C1 1 01C2201 .ICV(1)=OV(2)=0.4.IRAN 0.1s 40s SKIPBPПеременные x 1 = V(l), x 2 = V(2).
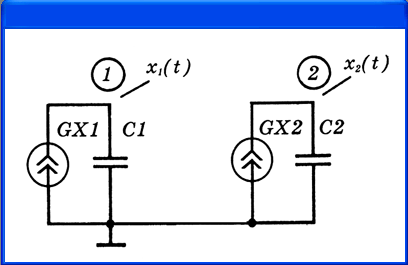
Рис. 4.19. Моделирование системы двух дифференциальных уравнений
