Анализируем спектр сигнала
Команды View › Multitrack View, View › Waveform View и View › Spectral View переключают режимы отображения звуковой информации. Первому из перечисленных режимов посвящена гл. 10. Со вторым режимом вы уже знакомы, в нем мы работали до сих пор. В этих двух режимах звук представляется в виде волновых форм. Последняя команда включает режим отображения мгновенного спектра сигнала в виде градаций яркости и цвета.
Знакомимся со спектральным анализом
О спектральной форме представления сигнала и, в частности, о мгновенном спектре детально рассказывается в книге [12]. Здесь же мы ограничимся лишь пояснениями, необходимыми для понимания сути спектрального анализа и основных терминов.
Классический спектр
Начать знакомиться с сущностью спектральных представлений лучше с разложения в ряд Фурье периодического сигнала. Всякая периодическая функция (с ограничениями, носящими абстрактный характер) может быть представлена в виде разложения в ряд по тригонометрическим функциям – суммой слагаемых, каждое из которых есть не что иное, как косинусоидальное колебание с амплитудой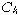 
и начальной фазой 
.
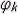Совокупность коэффициентов 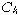называется амплитудным спектром сигнала, а 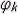– его фазовым спектром.
Частоты всех синусоидальных колебаний, из которых составляется периодическая функция s(t), кратны основной частоте F = 1/T. Отдельные составляющие называются гармониками. Колебание с частотой F называется первой гармоникой (к = 1), с частотой 2F– второй гармоникой (к = 2) и т. д.
Ряд Фурье дает разложение периодической функции по тригонометрическим функциям. Это разложение можно применить и к непериодической функции, которую рассматривают как предельный случай периодической функции при неограниченном возрастании периода. Если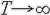 
, то 
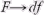, а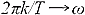 
(параметр 
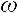– круговая текущая частота, изменяющаяся непрерывно) и ряд Фурье превращается в интеграл Фурье. Непериодическая функция может быть представлена только суммой бесконечно большого числа бесконечно близких по частоте колебаний с бесконечно малыми амплитудами. Интеграл Фурье представляет непериодическую функцию суммой синусоид и косинусоид с непрерывной последовательностью частот. Иногда говорят, что в составе непериодического сигнала есть колебания всех частот. В случае непериодического сигнала говорить об амплитудах отдельных спектральных составляющих нет смысла, т. к. это бесконечно малые величины.
Текущий спектр
Классическое определение спектра основывается на преобразовании Фурье, причем интегрирование по времени выполняется в бесконечных пределах и спектр зависит только от частоты. Однако бесконечная длительность какого-либо процесса – это абстракция, не имеющая ничего общего с реальностью.
Если анализируемая функция есть отображение некоторого реального физического процесса, то сведения о спектре мы получаем лишь в результате наших наблюдений. Следовательно, при анализе спектра мы можем выполнить вычисления лишь от момента начала наблюдения до текущего момента времени t, а не до момента, устремленного в бесконечное будущее.
Текущий спектр определяется как результат преобразования Фурье, но с переменным верхним пределом интегрирования, в качестве которого фигурирует текущее время. Поэтому текущий спектр является функцией не только частоты, но и времени.
В начале раздела мы воспользовались понятием периодической функции. На самом деле периодическая функция – лишь весьма полезная математическая абстракция. Ведь всякий природный процесс имеет начало и конец.
Принято называть реальный циклический процесс периодическим, если он длится достаточно долго. Мерилом длительности служит число "периодов", которое должно быть намного больше единицы. Периодичность процесса проявляется лишь с течением времени, когда прорисовываются его характерные черты. Текущий спектр и отражает это развитие процесса. Таким образом, периодический процесс – это предел, к которому может стремиться с течением времени реальный повторяющийся процесс. Аналогично и спектр (в его классическом определении) такого процесса есть предел, к которому стремится текущий спектр при увеличении времени интегрирования до бесконечности. Например, при интегрировании в бесконечных пределах спектр синусоиды представляет собой единственную линию на частоте, равной частоте этой синусоиды.
Но как на практике измеряется текущий спектр, например, той же синусоиды? Мы включаем анализатор спектра, а спустя какое-то время выключаем его. Получается, что измеряется не спектр бесконечного синусоидального колебания, а спектр его более или менее протяженного отрезка. Это значит, что фактически исследуется спектр прямоугольного импульса с синусоидальным заполнением. Сказанное объясняет причину того, что даже для синусоидального колебания при уменьшении времени интегрирования спектральная линия расширяется, появляются боковые лепестки спектральной функции, ее нули все больше удаляются друг от друга. Ведь именно так и должен вести себя спектр прямоугольного импульса при уменьшении его длительности [12].
Таким образом, текущий спектр в большей степени отражает свойства сигналов, проявляющиеся в реальных условиях их генерирования и обработки, нежели спектр, полученный на бесконечном временном интервале.
Мгновенный спектр
Текущий спектр – только мостик от частотного к временному описанию процесса. Не только спектр, вычисленный на бесконечном временном интервале, но и текущий спектр – слишком грубый инструмент в тех случаях, когда анализируемый процесс не стационарен. Для того чтобы сблизить частотное и временное представления сигнала, было введено понятие мгновенного спектра. Мгновенный спектр – это спектр короткого отрезка процесса, непосредственно предшествующего данному моменту времени. В этом определении мы имеем дело со скользящим интегрированием: интервал интегрирования имеет постоянную длину, но перемещается по оси времени. А вот относительно текущего времени этот интервал расположен неизменно. Страшно далеко это определение спектра от того, что давно придумали великие математики! И все же в руках звукорежиссера именно мгновенный спектр является наиболее эффективным инструментом анализа свойств записываемого или уже записанного звука. Музыка, которую создают с помощью синтезатора, отличается особенно заметной нестационарностью тембра. Может быть, именно поэтому в звуковых редакторах уже давно используются средства анализа текущего и мгновенного спектра.