Сортировка
При разделении прежде всего случайным образом выбирается элемент-разделитель, который временно переставляется в начало массива, затем просматриваются остальные. Элементы, меньшие разделителя ("маленькие" элементы), перемещаются ближе к началу массива (на позицию last), а "большие" элементы – в сторону конца массива (на позицию i). В начале процесса, сразу после перемещения разделителя в начало, last = 0 и элементы с i = 1 по n-1 еще не исследованы:

В начале 1-й итерации элементы с первого по last строго меньше разделителя, элементы с last+1 по i-1 больше или равны разделителю, а элементы с i по n-1 еще не рассмотрены. Пока не выполнилось первый раз условие v[i] >='v[0], алгоритм будет переставлять элемент v[i] сам с собой; это, конечно, занимает дополнительное время, но не столь страшно.

Когда все элементы просмотрены, нулевой элемент переставляется на позицию last, чтобы разделитель занял свою окончательную позицию; тогда порядок элементов будет правильным. Теперь массив выглядит так:
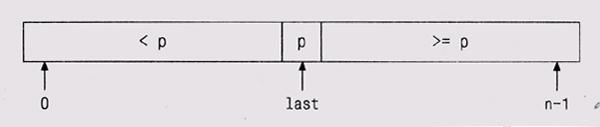
Та же самая операция применяется к левой и правой частям массива; после окончания этого процесса весь массив будет отсортирован.
Насколько быстро работает быстрая сортировка? В наилучшем случае:
- первый проход делит массив из п элементов на две группы примерно по n/2 элементов;
- второй проход разделяет две группы по n/2 элементов на 4 группы, в каждой из которых примерно по n/4 элементов;
- на следующем проходе четыре группы по n/4 делятся на восемь групп по (примерно) n/8 элементов;
- и т. д.
Данный процесс продолжается примерно Iog2n раз, поэтому общее время работы в лучшем случае пропорционально n + 2 X n/2 + 4 х и/4 + + 8 X n/8… (Iog2 и слагаемых), что равно nlog2n. В среднем алгоритм работает совсем не намного дольше. Обычно принято использовать именно двоичные логарифмы, поэтому мы можем сказать, что быстрая сортировка работает пропорционально nlong.
Эта демонстрационная реализация быстрой сортировки наиболее прозрачна, но у нее есть одна слабина. Если каждый выбор разделителя разбивает массив на две примерно одинаковые группы, то наш анализ корректен, однако если разделение слишком часто происходит неровно, то время работы будет расти скорее как n1. В нашей реализации в качестве разделителя берется случайный элемент, чтобы уменьшить шанс того, что плохие входные данные приведут к слишком большому количеству неровных разбиений массива. Но если все входные значения одинаковы, то наша реализация за каждый проход будет отделять только один элемент, поэтому время работы будет расти как n2.
Поведение некоторых алгоритмов сильно зависит от входных данных. Неправильный или неудачный ввод может заставить в среднем хороший алгоритм работать крайне медленно или использовать огромное количество памяти. В случае быстрой сортировки, хотя простые реализации вроде нашей иногда могут работать медленно, более продуманные реализации способны уменьшить шанс патологического поведения почти до нуля.
