Деревья
Дерево – иерархическая структура данных, хранящая набор элементов. Каждый элемент имеет значение и может указывать на ноль или более других элементов. На каждый элемент указывает только один другой элемент. Единственным исключением является корень дерева, на который не указывает ни один элемент. Входящие в дерево элементы называются его вершинами.
Есть много типов деревьев, которые отражают сложные структуры, например деревья синтаксического разбора (parse trees), хранящие синтаксис предложения или программы, либо генеалогические деревья, описывающие родственные связи. Мы продемонстрируем основные принципы на деревьях двоичного поиска, в которых каждая вершина (node) имеет по две связи. Они наиболее просто реализуются и демонстрируют наиболее важные свойства деревьев.
Вершина в двоичном дереве имеет значение и два указателя, left и right, которые показывают на его дочерние вершины. Эти указатели могут быть равны null, если у вершины меньше двух дочерних вершин. Структуру двоичного дерева поиска определяют значения в его вершинах: все дочерние вершины, расположенные левее данной, имеют меньшие значения, а все дочерние вершины правее – большие. Благодаря этому свойству мы можем использовать разновидность двоичного поиска для быстрого поиска значения по дереву или определения, что такого значения нет.
Вариант структуры Nameval для дерева пишется сразу:

Комментарии "большие" и "меньшие" относятся к свойствам связей: левые "дети" хранят меньшие значения, правые – большие.
В качестве конкретного примера на приведенном рисунке показано подмножество таблицы символов в виде дерева двоичного поиска для структур Nameval, отсортированных по ASCII-значениям имен символов.
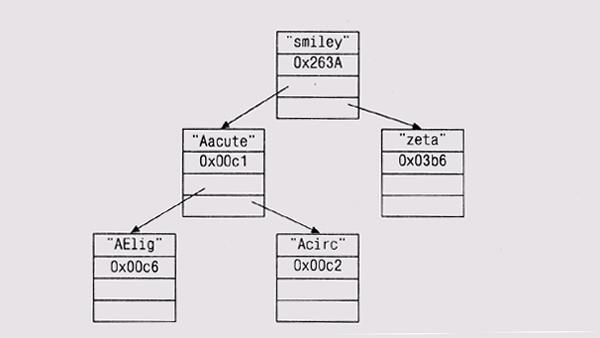
Поскольку в каждой вершине дерева хранится несколько указателей на другие элементы, то многие операции, занимающие время порядка О(n) в списках или массивах, занимают только O(log n) в деревьях. Наличие нескольких указателей в каждой вершине сокращает время выполнения операций, так как уменьшается количество вершин, которые необходимо посетить, чтобы добраться до нужной.
