Использование различных алгоритмов в системе Mathematica
Mathematica автоматически выбирает соответствующие алгоритмы для каждого вычисления.
FindRoot[Cos[x]==x+Log[x],{x,1}]
{x->0.840619}
NIntegrate[Log[x+Sin[x]],{x,0,2}]
0.555889
NSolve[x^5-6x^3+8x+1==0,x]
{{x->-2.05411},{x->-1.2915},{x->-0.126515}, {x->1.55053},{x->1.9216}}
Mathematica использует современные алгоритмы для разложения на множители целых чисел. Результат приведен в виде списка сомножителей и соответствующих показателей степеней.
FactorInteger[2^105-1]
{{7,2},{31,1},{71,1},{127,1},{151,1},{337,1}, {29191,1},{106681,1},{122921,1},{152041,1}}
Эта команда генерирует двумерную таблицу.
m=Table[2^i + x^j,{i,3},{j,4}]
{{2+x,2+x2,2+x3,2+x4},{4+x,4+x2,4+x3,4+x4}, {8+x,8+x2,8+x3,8+x4}}
Представление таблицы в форме матрицы.
MatrixForm[m]
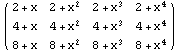
Вычисление ядра матрицы.
NullSpace[m]
{{x+x2,-1-x-x2,0,1},{x,-1-x,1,0}}
Mathematica может решать дифференциальные уравнения как численно, так и в аналитической форме.
Ниже Mathematica численно решает нелинейное дифференциальное уравнение. Ответ – интерполяционная функция, которая представляет решение в неявной форме.
NDSolve[{x''[t]+x[t]^3==Sin[t],x[0]==x'[0]==0},x, {t,0,50}]
{{x->InterpolatingFunction[{{0.,50.}},<>]}}
Параметрический график решения. Команда /. означает, что Mathematica должна подставить предыдущее решение вместо x[t].
ParametricPlot[Evaluate[{x[t],x'[t]}/.%],{t,0,50}]
-Graphics-
