Написание программ в системе Mathematica
Язык программирования высокого уровня системы Mathematica позволяет Вам писать сложные программы быстрее, чем когда-либо прежде.
Даже состоящая всего из одной строки программа системы Mathematica может выполнять сложные операции.
Эта программа моделирует одномерное случайное блуждание.
RandomWalk[n_]:=NestList[(#+(-1) ^Random[Integer])&,0,n]
График, демонстрирующий первые 200 шагов случайного блуждания.
ListPlot[RandomWalk[200],PlotJoined->True];
Ясность программ системы Mathematica позволяет легко модифицировать их для более общих случаев.
Эта программа моделирует случайное блуждание в пространстве размерности d.
RandomWalk[n_,d_]:=NestList[(#+(-1) ^Table[Random[Integer],{d}])&,Table[0,{d}],n]
График трехмерного случайного блуждания.
Show[Graphics3D[Line[RandomWalk[1000,3]]]];
Богатство языка программирования системы Mathematica делает простой реализацию сложнейших алгоритмов.
Это программа для моделирования одного шага эволюции клеточной системы.
LifeStep[a_List] := MapThread[If[(#1 == 1 && #2 == 4) || #2 == 3, 1, 0]&,
{a, Sum[RotateLeft[a, {i, j}], {i, -1, 1}, {j, -1, 1}]}, 2]
А это пример оптимизированной программы, которая оперирует со списками живых клеток.
LifeStep[list_] := With[{u=Split[Sort[Flatten[Outer[Plus,list,N9,1] ,1]]]},
Union[Cases[u,{x_,_,_}->x], Intersection[Cases [u,{x_,_,_,_}->x],list]]]
N9=Flatten[Array[List,{3, 3},-1], 1] ;
Система Mathematica позволяет легко создавать программы, состоящие из нескольких компонент.
Здесь приведены составляющие программы, моделирующей поведение клеточных систем.
CenterList[n_Integer]:=ReplacePart[Table[0, {n}], 1, Ceiling[n/2]]
ElementaryRule [num_Integer] := IntegerDigits[num, 2, 8]
CAStep[rule_List, a_List] :=rule[[ 8 - (RotateLeft[a] + 2 (a + 2 RotateRight[a])) ]]
CAEvolveList[rule_List, init_List, t_Integer] :=NestList[CAStep[rule, #]&, init, t]
CAGraphics[history_List] :=Graphics[Raster[1 - Reverse[history]], AspectRatio -> Automatic]
Пример работы программы.
Show[CAGraphics[ CAEvolveList[ElementaryRule[30], CenterList[101], 50]] ];
Mathematica имеет компилятор для оптимизации программ, которые работают со списками и числами.
CAStep = Compile[{{rule, _Integer, 1}, {a, _Integer,1}},
rule[[ 8 - (RotateLeft[a] + 2 (a + 2 RotateRight[a])) ]]]
Программы системы Mathematica зачастую являются прямой трансляцией теоретических положений справочной литературы.
Здесь вводятся необходимые определения для расчета импеданса электрической цепи.

Использование данных выше определений.
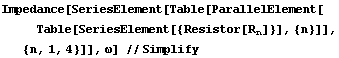
Пример электрической схемы, заданной при помощи символической спецификации.