Объединяющая идея системы Mathematica
Единая форма записи символических выражений дает возможность вводить в системе Mathematica любую конструкцию, которая Вам необходима.
Химическая формула.
HNO3
Chemical[{Hydrogen,1},{Nitrogen,1},{Oxygen,3}]
Электрическая цепь.
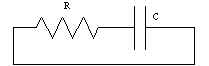
Circuit[{Resistor["R"],Capacitor["C"]}]
Все операции в системе Mathematica в конечном счете – преобразования символических выражений. Mathematica имеет уникальную возможность работы с шаблонами при проведении преобразований.
Команда /. служит сигналом системе Mathematica применить подстановку b › 1 + x.
{a,b,c,d}/.b->1+x
{a,1+x,c,d}
Каждый символ x_ и y_ замещает любое выражение, так что шаблон x _ + y_ обозначает собой сумму любых двух объектов.
{a + b, c + d, a + c} /. x_ + y_ -> x2 + y2
{a2 + b2, c2 + d2, a2 + c2}
{a + b, c + d, a + c} /. a + x_ -> x3
{b3, c + d, c3}
Mathematica использует шаблоны, чтобы обобщить понятие функции.
Это стандартный способ определения функции для всех значений x.
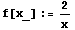
Изменение общего определения функции при фиксированном значении аргумента.
f[0]:=e
Пример использования определенной выше функции f.
f[6]+f[a+b]+f[0]
Сброс определения функции f.
Clear[f]
Важная особенность использования шаблонов заключается в том, что они позволяют определять операции, аргументами которых могут выступать любые объекты.
Определение функции g, аргументом которой является список, состоящий из двух элементов.
g[{x_,y_}]:=x+y
g[{4,a b}]
4+a b
Clear[g]
Определение функции, имеющей смысл площади круга, аргументом которой является объект Circle.
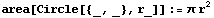
area[Circle[{2,3},u]]
Осуществление преобразования логического правила.
reduce[p_ && q_ || p_]:=p
