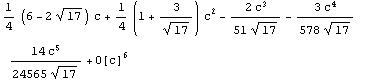Конструирование вычислений
Возможность манипулировать различными формулами и их фрагментами позволяет Вам легко интегрировать любые части вычислений.
Вычисление собственных чисел матрицы.
Eigenvalues[{{3, 1}, {2, 6}}]
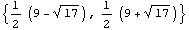
Система Mathematica способна вычислять собственные значения даже тогда, когда элементы матрицы являются символьными параметрами. В результате получается компактное представление собственных чисел для любого значения b.
v = Eigenvalues[{{3, 1}, {2, b}}]
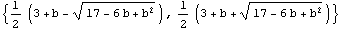
Встроенные функции системы Mathematica разработаны так, чтобы любые результаты выполнения предыдущих операций могли быть легко использованы как исходные данные для последующих.
Использование предыдущего результата для построения графиков функций, задающих собственные значения, в зависимости от параметра.
Plot[Evaluate[v], {b, -10, 10}]
-Graphics-
Вы можете найти значение b, при котором первое собственное значение равно нулю…
Solve[First[v] == 0, b]
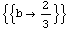
…или найти интеграл от 0 до с от функции, задающей первое собственное значение.

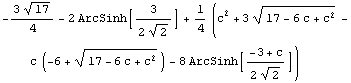
Теперь можно найти частичную сумму ряда Тейлора функции, являющейся результатом предыдущего интегрирования.
Series[%, {c, 0, 5}]