Иллюстрированный самоучитель по созданию чертежей

Пересечение поверхности с плоскостью. Тела с вырезами.

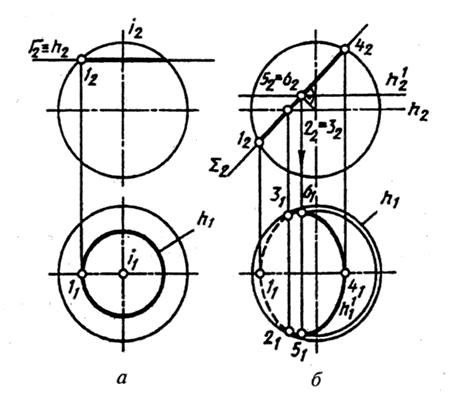
Рис. 126

При пересечении сферы плоскостью всегда получается окружность. Если секущая плоскость параллельна какой-либо плоскости проекций, то на эту плоскость окружность сечения проецируется без искажения (рис. 126, а). Если секущая плоскость занимает проецирующее положение, то на плоскости проекций, которой секущая плоскость перпендикулярна (рис. 126, б – на фронтальной), окружность сечения изображается отрезком прямой (1₂– 4₂), длина которого равна диаметру окружности, а на другой плоскости – эллипсом, большая ось которого (5₁– 6₁) равна диаметру окружности сечения. Этот эллипс строят по точкам. Точки видимости 2 и 3 относительно плоскости П₁ лежат на экваторе сферы.

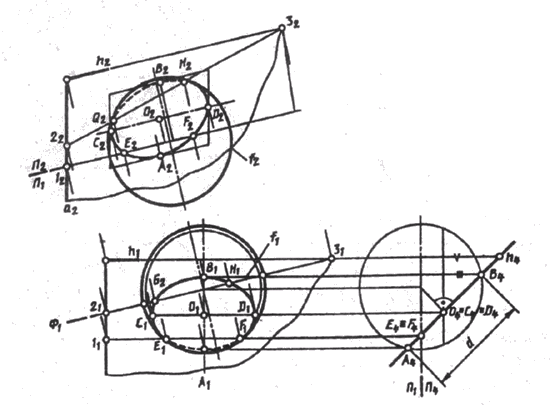
Рис. 127

Задача построения линии пересечения несколько сложнее при пересечении сферы плоскостью общего положения (рис. 127) Q (a^h).

Этот случай можно свести к предыдущему (см. рис. 126, б), если построить дополнительные изображения сферы и секущей плоскости на плоскости П₄ _|_П₁, причем П₄ _|_ h (6). Тогда плоскость в станет проецирующей Q _|_П₄ в новой системе плоскостей (см. рис. 127). На чертеже оси проекции проходят через центр сферы. На плоскости П₄ отмечаем проекции опорных точек: А₄ – самой низкой точки сечения; В ₄ – самой высокой, дающих величину диаметра d окружности сечения с центром в точке О (О₄); Е₄ = F₄ – на экваторе сферы– точек видимости линии сечения относительно плоскости П₁, С₄ = D₄ = O₄ – горизонтального диаметра CD, определяющего большую ось эллипса, – горизонтальной проекции окружности сечения. Горизонтальная проекция сечения – эллипс – легко строится по большой C₁D₁ и малой А₁В₁ осям. Фронтальная проекция окружности тоже эллипс, который можно построить по сопряженным диаметрам A₂B₂ и C₂D₂ (высоты этих точек отмечены на плоскости П₂ и на плоскости П₄) с помощью описанного параллелограмма. Видимость окружности сечения относительно плоскости П₂ определяется точками G и H, полученными в пересечении главного меридиана сферы f с плоскостью 9. Для этого взята вспомогательная плоскость уровня Ф:

Ф э f; Ф ^ Q = 2-3;

f ₂^2₂– 3₂ = H₂ и G₂.

Линии среза получаются при пересечении поверхности вращения плоскостью, параллельной оси вращения поверхности. Линии среза часто встречаются на поверхностях деталей. На рис. 128 построена линия среза комплексной поверхности, состоящей из поверхностей сферы и конуса, фронтальной плоскостью уровня Ф. Линия среза включает линию пересечения сферы (В₂ – А₂ – С₂) – часть окружности радиуса r– и линию пересечения конуса (В₂ – D₂ – С₂) – ветвь гиперболы, которую строят по отдельным точкам. В качестве вспомогательных секущих плоскостей для построения промежуточных точек берут плоскости, перпендикулярные оси вращения поверхностей.