Иллюстрированный самоучитель по созданию чертежей

Пересечение поверхности с плоскостью. Тела с вырезами.

При пересечении поверхности с плоскостью в сечении получают плоскую линию. Эту линию строят по отдельным точкам. В начале построения сперва выявляют и строят опорные точки, лежащие на контурных линиях поверхности, а также точки на ребрах и линиях основания поверхности. В тех случаях, когда проекция линии пересечения не полностью определяется этими точками, строят дополнительные, промежуточные точки, расположенные между опорными.

В данном разделе рассматриваются случаи пересечения поверхности плоскостями частного положения, так как в случае наличия секущей плоскости общего положения чертеж всегда можно преобразовать так, чтобы секущая плоскость стала проецирующей (см. рис. 129).

В случае пересечения гранной поверхности плоскостью получается плоская ломаная линия. Чтобы построить эту линию, достаточно определить точки пересечения плоскостью ребер и сторон основания, если имеет место пересечение основания, и соединить построенные точки с учетом их видимости (рис. 124, а). Так как в этом случае секущая плоскость Е занимает фронтальное проецирующее положение, то точки пересечения ребер определяются без дополнительных построений:

AS^Sum=1(1₂; l₁); Sum = (2₂; 2₁); CS^Sum = 3(3₂; 3₁).

Так как грань ACS относительно плоскости П\ невидима, то и линия l₁– 3₁ тоже невидима.

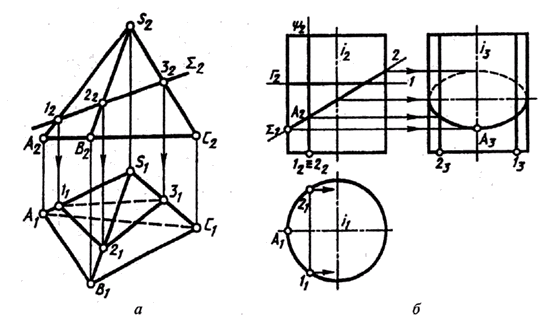
Рис. 124

В случае пересечения цилиндрической поверхности вращения плоскостью могут быть получены следующие линии (рис. 124, б):

• окружность, если секущая плоскость Г перпендикулярна оси вращения поверхности;
• эллипс, если секущая плоскость Sum не перпендикулярна и не параллельна оси вращения;
• две образующие прямые, если секущая плоскость U параллельна оси поверхности.

На плоскость П₁, перпендикулярную оси вращения поверхности, окружность и эллипс на поверхности цилиндра проецируются в окружность, совпадающую с проекцией всей поверхности.

При пересечении конической поверхности вращения плоскостью могут быть получены следующие линии (рис. 125, а – д):

• окружность, если секущая плоскость Г перпендикулярна оси вращения (а);
• эллипс, если секущая плоскость Sum¹ пересекает все образующие поверхности (б);
• парабола, если секущая плоскость (Sum²) параллельна только одной образующей (S – 1) поверхности (в);
• гипербола, если секущая плоскость (Sum³) параллельна двум образующим (S– 5 и 5-6) поверхности (г);
• две образующие (прямые), если секущая плоскость (Sum⁴) проходит через вершину S поверхности (д).

Проекции кривых линий сечений плоскостью конуса строятся по отдельным точкам (точки 2, 4 на рис. 125, б).

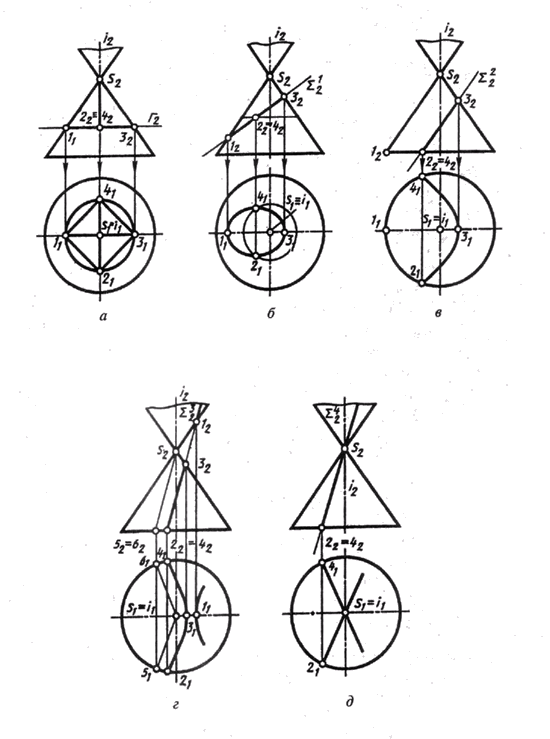
Рис. 125