Иллюстрированный самоучитель по созданию чертежей

Построение линии пересечения поверхностей способом вспомогательных сфер

Вспомогательные горизонтально или фронтально проецирующие плоскости, проведенные через вершину одной из поверхностей, будут пересекать их по образующим и эллипсам. В данном примере выполнены условия, позволяющие применение вспомогательных сфер для построения точек линии пересечения. Оси поверхностей вращения пересекаются в точке О (О₁; О₂), которая является центром вспомогательных сфер, радиус сферы изменяется в пределах Rmin < R < Rmах – Радиус максимальной сферы определяется расстоянием от центра О наиболее удаленной точки В (R_max = О₂В₂), а радиус минимальной сферы определяется как радиус сферы, касающейся одной поверхности (по окружности h²) и пересекающей другую (по окружности h³).

Плоскости этих окружностей перпендикулярны осям вращения поверхностей. В пересечении этих окружностей получаем точки Е и F, принадлежащие линии пересечения поверхностей:

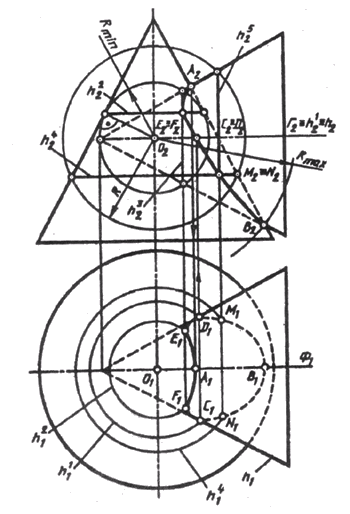
Рис. 135

h² ₂ ^ h³ ₂ = E₂(F₂); Е₂Е₁ || А₂А₁;

Е₂Е₁ ^ h² ₁ =E₁; F₂F ^ h₁ = F₁

Промежуточная сфера радиуса R пересекает поверхности по окружностям h⁴ и h⁵, в пересечении которых находятся точки М и N:

h⁴ ₂ ^ h⁵ ₂ = M₂(N₂); M₂M₁ || А₂А₁,

М₂М₁ ^ h⁴ ₁ = М₁; N₂N₁ ^ h⁴ ₁ = N₁

Соединяя одноименные проекции построенных точек с учетом их видимости, получаем проекции линии пересечения поверхностей.