Поиск пути
Механизм рекурсии весьма эффективен при программировании задач поиска. В качестве еще одного примера рассмотрим задачу поиска пути между двумя городами. Если несколько городов соединены дорогами, то очевидно, что попасть из одного города в другой можно различными маршрутами. Задача состоит в нахождении всех возможных маршрутов.
Карта дорог между городами может быть изображена в виде графа – набора вершин, означающих города, и ребер, обозначающих дороги (рис. 12.9).
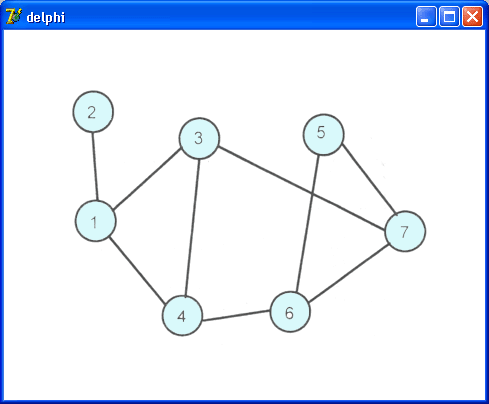
Рис. 12.9. Представление карты дорог в виде графа
Процесс поиска может быть представлен как последовательность шагов. На каждом шаге с использованием некоторого критерия выбирается точка, в которую можно попасть из текущей. Если очередная выбранная точка совпала с заданной конечной точкой, то маршрут найден. Если не совпала, то делаем из этой точки еще шаг. Так как текущая точка может быть соединена с несколькими другими, то нужен какой-то формальный критерий выбора. В простейшем случае можно выбрать точку с наименьшим номером.
Пусть, например, надо найти все возможные пути из точки 1 в точку 5. Согласно принятому правилу, сначала выбираем точку 2. На следующем шаге выясняем, что точка 2 тупиковая, поэтому возвращаемся в точку 1 и делаем шаг в точку 3. Из точки 3 – в точку 4, из 4 – в 6 и из точки 6 – в точку 5. Один маршрут найден. После этого возвращаемся в точку 6 и проверяем, возможен ли шаг в точку, отличную от 5. Так как это возможно, то делаем шаг в точку 7, и затем – в 5. Найден еще один путь. Таким образом, процесс поиска состоит из шагов вперед и возвратов назад. Поиск завершается, если из узла начала движения уже некуда идти.
Алгоритм поиска имеет рекурсивный характер: чтобы сделать шаг, мы выбираем точку и опять делаем шаг, и так продолжаем до тех пор, пока не достигнем цели.
Таким образом, задача поиска маршрута может рассматриваться как задача выбора очередной точки (города) и поиска оставшейся части маршрута, т. е. имеет место рекурсия.
Граф можно представить двумерным массивом, который назовем тар (карта). Значение элемента массива map[i, j] – это расстояние между городами i и j, если города соединены дорогой, или ноль, если города не соединены прямой дорогой. Для приведенного графа массив тар можно изобразить в виде таблицы, представленной на рис. 12.10.
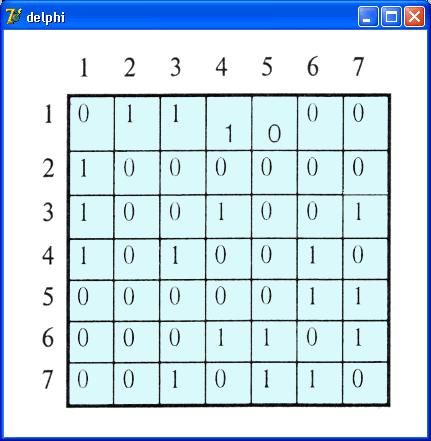
Рис. 12.10. Массив тар
