Иллюстрированный самоучитель по созданию чертежей

Определение натуральной величины отрезка прямой линии

При решении задач инженерной графики в ряде случаев появляется необходимость в определении натуральной величины отрезка прямой линии. Решить эту задачу можно несколькими способами: способом прямоугольного треугольника, способом вращения, плоскопараллельного перемещения, заменой плоскостей проекций.

Рассмотрим пример построения изображения отрезка в истинную величину на комплексном чертеже способом прямоугольного треугольника. Если отрезок расположен параллельно какой-либо из плоскостей проекций, то на эту плоскость он проецируется в натуральную величину. Если же отрезок представлен прямой общего положения, то на одной из плоскостей проекций нельзя определить его истинную величину (см. рис. 69).

Возьмем отрезок общего положения АВ (A ^ П₁) и построим его ортогональную проекцию на горизонтальной плоскости проекций (рис. 78, а). В пространстве при этом образуется прямоугольник А₁ВВ₁, в котором гипотенузой является сам отрезок, одним катетом – горизонтальная проекция этого отрезка, а вторым катетом – разность высот точек А и В отрезка. Так как по чертежу прямой определить разность высот точек ее отрезка не составляет труда, то можно построить по горизонтальной проекции отрезка (рис. 78, б) прямоугольный треугольник, взяв вторым катетом превышение одной точки над второй. Гипотенуза этого треугольника и будет натуральной величиной отрезка АВ.

Аналогичное построение можно сделать на фронтальной проекции отрезка, только в качестве второго катета надо взять разность глубин его концов (рис. 78, в), замеренную на плоскости П₁.

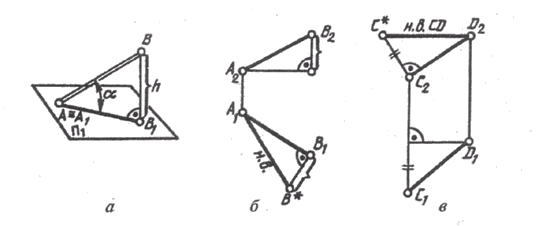
Рис. 78

Для определения натуральной величины отрезка прямой можно воспользоваться поворотом ее относительно плоскостей проекций, чтобы она расположилась параллельно одной из них, или вводом новой плоскости проекций (заменой одной из плоскостей проекций) так, чтобы она была параллельна одной из проекций отрезка.