Иллюстрированный самоучитель по созданию чертежей

Взаимное расположение двух прямых

Две прямые пространства могут иметь различное расположение (рис. 74). Они могут совпадать а = b, быть параллельными c|| d, пересекаться т ^ n и скрещиваться (k° / l).

Если две прямые параллельны, то на комплексном чертеже (рис. 75, а) их одноименные проекции параллельны.

Если две прямые пересекаются в некоторой точке М, то проекции этой точки должны принадлежать одноименным проекциям прямых, т. е. точки пересечения одноименных проекций пересекающихся прямых должны лежать на одной линии связи (рис. 75, б):

m^n=M › {m₁^n₁=M₁ или m₂^n₂= М₂}

Если две прямые скрещиваются, то их одноименные проекции могут пересекаться в точках, не лежащих на одной линии связи (рис. 75, в):

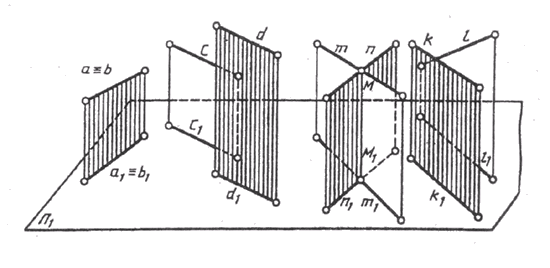
Рис. 74

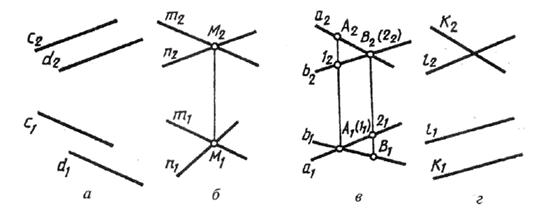
Рис. 75

a°/b › а₁ ^ b₁= А₁(l₁) – горизонтально конкурирующие точки; а₂^b₁ = В₂(l₁) – фронтально конкурирующие точки.

В другом случае одна пара проекций будет пересекаться, а вторая может быть параллельными прямыми (рис. 75, г):

k⁰ /l › { k₂ ^ l₂ или k₁ || l₁}