Иллюстрированный самоучитель по созданию чертежей

Прямоугольные координаты точек

Три основные плоскости проекций (П₁_|_П ₂ _|_ П₃) могут рассматриваться и как координатные плоскости. Тогда оси проекций становятся координатными осями: осью абсцисс х, П₁/П₃ – осью координат у, П₂/П₃ – осью аппликат z.

Начало координат (точка О) располагается в точке пересечения осей координат (рис. 68, а).

Чтобы отнести точку А к натуральной системе координат Oxyz, надо построить ортогональную проекцию точки А на плоскости хОу. Затем проекцию А₁ ортогонально проецировать на ось х в точку А_х. Тогда получим пространственную координатную ломаную АА₁А_ХО, отрезки которой параллельны осям координат и соответственно называются: ОА_Х – отрезком абсциссы; А_Х А₁ – отрезком ординат; А₁А – отрезком аппликаты.

Измерив координатные отрезки единицей длины l, получим три отвлеченных числа – три координаты точки А:

х = OA_X абсцисса; у = A_xA₁– ордината; z = AA₁– аппликата.

Если точка задана своими координатами А (х, у, z), то можно построить ее комплексный чертеж, задав соответствующую единицу длины l (например, l = 1 мм). Абсцисса точки определяет положение вертикальной линии связи (рис. 68, б). Горизонтальная проекция точки определяется величиной ординаты, а фронтальная – величиной аппликаты.

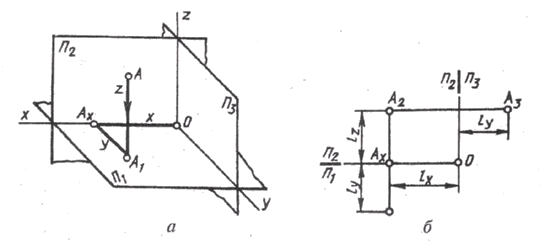
Рис. 68