Кривая Безье
В качестве формулы, которая была бы достаточно простой (с точки зрения математика), универсальной (с точки зрения программиста) и геометрически наглядной (с точки зрения пользователя – художника или дизайнера), чаще всего используется упомянутая кривая Безье. На самом деле, это целое семейство кривых, из которых используется частный случай с кубической степенью, т. е. кривая третьего порядка, описываемая следующим параметрическим уравнением:
R (t)= P 0 (1-t)3 + P 1 (1-t)2 + P 2 t2 (1-t) + P 3 t3
Где 0_< t _<1.
Общий вид элементарной кривой Безье представлен на рис. П2.1. Такую кривую можно построить, если известны координаты четырех точек, называемых контрольными.
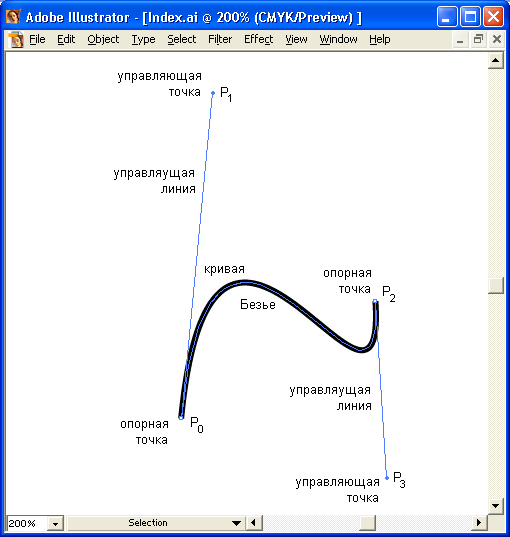
Рис. П2.1. Общий вид элементарной кривой Безье
Из четырех контрольных точек кривая проходит только через две, поэтому эти точки называются опорными – anchor points (иначе они именуются узлами (nodes), поскольку "связывают" элементарные кривые друг с другом, чтобы образовать единый сложный контур).
Две другие контрольные точки не лежат на кривой, но их расположение определяет кривизну кривой, поэтому эти точки иначе называются управляющими точками, а линии, соединяющие управляющую и опорную точки, – управляющими линиями (в просторечии именуются "рычагами").
Кривая Безье является гладкой кривой, т. е. она не имеет разрывов и непрерывно заполняет отрезок между начальной и конечной точками.
Кривая начинается в первой опорной точке, касаясь отрезка своей управляющей линии, и заканчивается в последней опорной точке, также касаясь отрезка своей управляющей линии. Это позволяет гладко соединять две кривые Безье друг с другом: управляющие линии располагаются вдоль одной прямой, которая является касательной к получившейся кривой (рис. П2.2).
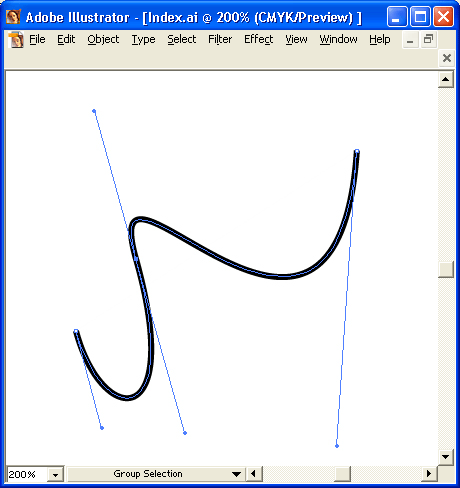
Рис. П2.2. Гладкое соединение двух кривых Безье
