Построение в одном окне графиков нескольких функций
Более подробное описание графического окна будет дано в уроке 5. А пока пойдем дальше и попытаемся построить графики сразу трех функций: sin(x), cos(#) и sin(x)/х. Прежде всего отметим, что эти функции могут быть обозначены переменными, не имеющими явного указания аргумента в виде у(х):
>>y1=sin(x); y2=cos(x); y3=sin(x)/x;Такая возможность обусловлена тем, что эти переменные являются векторами – как и переменная х. Теперь можно использовать одну из ряда форм команды:
plot: plot(a1.f1.a2.f2.a3.f3,...).Где a1, а2, а3, … – векторы аргументов функций (в нашем случае все они – х), а f1, f2, f3,… – векторы значений функций, графики которых строятся в одном окне. В нашем случае для построения графиков указанных функций мы должны записать следующее:
>> plot(x,y1,x,y2,x.y3)Можно ожидать, что MATLAB в этом случае построит, как обычно, точки графиков этих функций и соединит их отрезками линий. Но, увы, если мы выполним эти команды, то никакого графика не получим вообще. Не исключен даже сбой в работе программы. Причина этого казуса уже обсуждалась в предыдущем уроке – при вычислении функции y3=sin(x)/x, если х представляет собой массив (вектор), то нельзя использовать оператор матричного деления /.
Этот пример еще раз наглядно указывает на то, что чисто поверхностное применение даже такой мощной системы, как MATLAB, иногда приводит к досадным срывам. Чтобы все же получить график, надо вычислять отношение sin(x) x хс помощью оператора поэлементного деления массивов ./. Этот случай поясняет рис. 3.2.
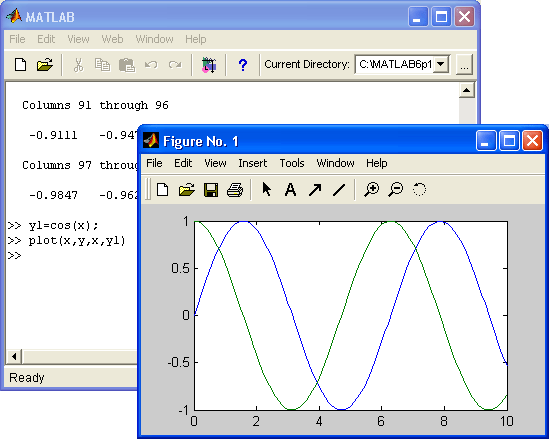
Рис. 3.2. Построение графиков трех функций
Обратите внимание на то, что хотя на этот раз MATLAB построил графики всех трех функций, в окне командного режима появилось предупреждение о делении на 0 – в момент, когда х=0. Это говорит о том, что plot "не знает" о том, что неопределенность sin(x)/x=0/0 устранимая и дает 1. Это недостаток практически всех систем для численных вычислений.
