Эллипсы
Для построения эллиптической дуги нужно в команде ELLIPSE (ЭЛЛИПС) в ответ на запрос первой точки выбрать опцию Arc (Дуга). Такому же варианту работы команды соответствует кнопка 
панели Draw (Рисование), а также пункт падающего меню Draw › Ellipse Arc (Рисование › Эллипс Дуга). Следующий запрос системы AutoCAD:
- Specify axis endpoint of elliptical arc or [Center]: (Конечная точка оси эллиптической дуги или [Центр]:) Далее: Specify other endpoint of axis: (Вторая конечная точка оси:)
Следующий запрос:
- Specify distance to other axis or [Rotation]: (Д/шна другой оси или [Поворот]:)
Теперь следует запрос на выделение дуги как части эллипса:
- Specify start angle or [Parameter]: (Начальный угол или /Параметр]:)
Начальный угол задается числом или с помощью мыши относительно первой оси (отсчет производится против часовой стрелки, начиная с первой точки оси). Далее:
- Specify end angle or [Parameter/Included angle]: (Конечный угол или [Параметр/Внутренний угол]:)
Можно задать конечный угол (рис. 2.108) или, выбрав опцию Included angle (Внутренний угол), ввести внутренний (центральный) угол дуги.
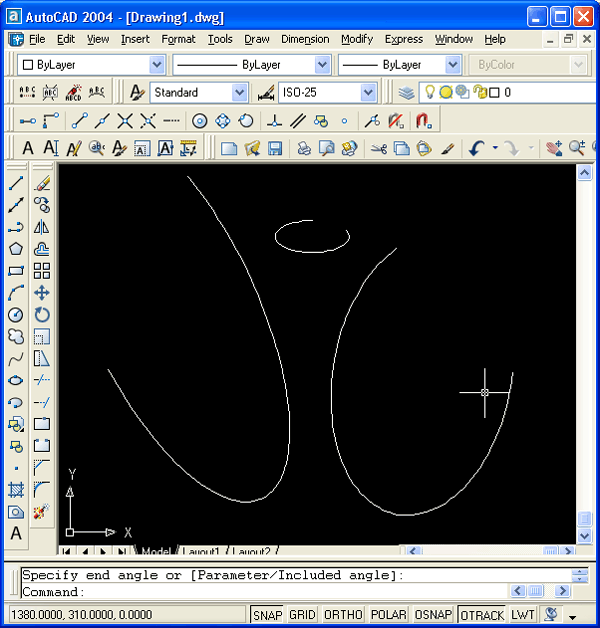
Рис. 2.108. Построение эллиптической дуги
Если вы в ответ на этот или иной запрос выбираете опцию Параметр (Parameter), то тогда вы задаете углы с помощью значения параметра в параметрическом векторном уравнении эллипса:
p(u) = c + acos(u) + bsin(u)Где с – это центр эллипса, а а и b – большая и малая оси эллипса (р, с, а и b – двумерные векторы); u – параметр уравнения.
Как начало, так и конец эллиптической дуги могут быть заданы углами или значениями параметра.