Разложение в ряд Тейлора по заданной переменной (Expand to Series…)
Операция Expand to Series… (Разложить в ряд) возвращает разложение в ряд Тейлора выражения относительно выделенной переменной с заданным по запросу числом членов ряда n (число определяется по степеням ряда). По умолчанию задано п=6. Разложение возможно для функции заданной переменной. В разложении указывается остаточная погрешность разложения. На рис. 8.16 представлено применение этой операции для разложения функции sin(x)/x. Минимальная погрешность получается при малых х (см. графическое представление функции и ее ряда).
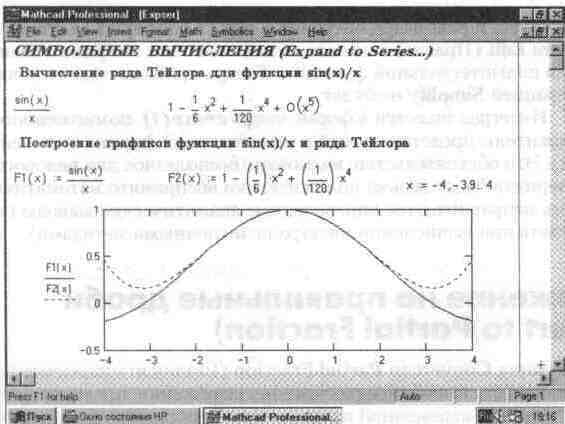
Рис. 8.16. Пример на разложение функции в ряд Тейлора
Символьные операции нередко можно комбинировать для решения сложных задач. Рис. 8.17 показывает интересное решение одной из таких задач – вычисление определенного интеграла, который не берется в замкнутой форме.

Рис. 8.17. Взятие определенного интеграла в символьной форме с заменой подынтегральной функции ее разложением
Если пользователя (например, инженера) интересует просто числовое значение интеграла, надо лишь поставить после интеграла знак вывода = и значение интеграла будет вычислено адаптивным численным методом Симпсона. Однако вычислить такой интеграл с помощью операции Simplify (Упростить) не удастся после долгих попыток система сообщит, что интеграл в замкнутой форме не берется.
Прием, который иллюстрирует рис. 8.17, заключается в замене подынтегральной функции ее разложением в ряд Тейлора. Вначале получим такое разложение с избытком – для 10 членов ряда (однако учтенных нечетных членов тут нет, такова специфика функции). Далее, выделив четыре первых реальных члена и используя операции Copy (Копировать) и Paste (Вставить) в позиции Edit (Правка) главного меню, поместим это разложение на место шаблона подынтегральной функции. Теперь проблем с вычислением интеграла операцией Simplify не будет.
Интеграл получен в форме числа е=ехр(1), помноженного на дробный множитель, представленный в рациональной форме (отношения целых чисел). Это обстоятельство, возможно, бесполезное для рядового пользователя, наверняка будет весьма положительно воспринято математиком, поскольку здесь напрашиваются определенные аналитические выводы (которых нельзя сделать при вычислении интеграла численными методами).
