Построение графиков функций
Строить графики в Бейсике мы будем точками, а задавать компьютеру функцию для построения оператором def fn.
Кроме того, координатная сетка экрана компьютера, как мы должны помнить, является перевернутой по отношению к привычной геометрической. Отсюда и последуют преобразования по приведению координатной сетки к нормальному виду. Я не хочу утомлять читателя длинными математическими выкладками, а призываю поверить на слово. Если же в ком-то проснется любознательность, то разобраться во всем можно самому.
Итак, оператор def fn определяет для компьютера ту функцию, график которой мы хотим построить. Работает он следующим образом:
DEF FN имя_функции{параметр_функции)=функция
Например, определим функцию у = sin x.
DEF FNY(X)=SIN(X)
Здесь y – имя функции, х – ее параметр, a sin (X) – непосредственно сама функция.
Определим функцию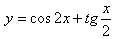 .
.
DEF FNY(X)=COS(2*X)+TAN(X/2)
Предупреждение
В одной и той же программе нельзя использовать для разных функций одно и то же имя. Необходимо давать разные имена, например Y(X), Z (X), R(X) И Т. Д.
Теперь непосредственно о построении графиков на примере функции синуса.
Сначала нарисуем оси координат – две взаимно перпендикулярные линии, пересекающиеся в центре экрана.
SCREEN 9 LINE (0, 175)-(640, 175), 15 LINE (320, 0)-(320, 350), 15 Rem ось абсцисс Rem ось ординат
Теперь определим функцию, как мы это уже делали.
DEF FNY(X)=SIN(X)
Далее самое интересное – загадочный цикл непосредственного построения графика.
FOR X=0 ТО 640 Y=175~30*FNY((X -320)/30) PSET(X, Y), 15 NEXT X
После запуска программы должна получиться следующая картинка (рис. 1.47).
Рис. 1.47. График функции синуса
Значение X изменяется от 0 до 640, давая возможность строить график на всю ширину экрана. Достаточно сложно выражение для Y. Это связано с переносом начала координат в центр экрана (отсюда числа 175 и 320). А вот число 30 в данном случае несколько произвольно – это коэффициент растяжения. Попробуйте его поменять сначала на 10, а потом на 50 (только менять всегда надо в двух местах) и посмотрите на возникающие отличия. На мой взгляд, коэффициент 30 наиболее оптимален.
Построение иного графика сводится к замене определения функции на другую.
