Циклы с несколькими зависимыми параметрами
Бывает, что при попытке выполнить задание с помощью оператора цикла выясняется, что изменяется не одна, а две или три величины. В том случае, если вы можете установить между ними зависимости, следует использовать следующие правила:
- определить, какие же величины изменяются, и обозначить их буквами;
- назначить одну из этих величин независимым аргументом;
- определить закономерности, связующие изменяющиеся величины, и выразить эти величины через независимый аргумент;
- написать программу с оператором цикла, основным параметром которого будет независимый аргумент, а в командах тела цикла, на месте других изменяющихся величин, необходимо подставить их выражения через этот независимый аргумент.
Приведем пример. Предположим, мы хотим построить семейство окружностей, как на рис. 1.49. Не правда ли, напоминает рупор?
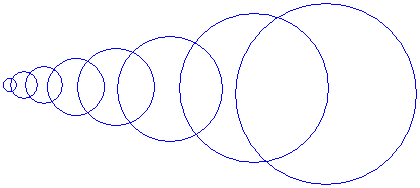
Рис. 1.49. "Рупор"
Действуем по правилам. Все окружности лежат на одной горизонтали, т. е. у их центров меняются не координаты Y, а координаты X. Кроме этого, они имеют разный радиус. Причем он изменяется не спонтанно, плавно увеличиваясь. Итак, обозначим изменяющиеся величины: X – координата центров окружностей по оси абсцисс, R – радиус окружностей.
Назначим независимым аргументом координату X. Попробуем установить закономерность изменения радиуса R от аргумента X. X изменяется от 0 до 640. Допустим, шаг изменения 10. Обычно устанавливают такое взаимоотношение X и R:
R=X
Но в этом случае получится, что радиус последней окружности будет равен 640, диаметр, соответственно, 1280. А ведь экран высотой всего 350! Значит, если мы хотим видеть на экране все наши окружности, то последний радиус не должен превышать 175, а лучше был бы меньше. Попробуем избрать такое соотношение:
R=X/4
Максимальное значение радиуса в таком случае равно 160. Напишем программу:
SCREEN 9 FOR Х=0 ТО 640 STEP 10 CIRCLE (X, 175), Х/4, 15 NEXT X
Посмотрите, что получается на экране. Похоже? Не совсем, скажете вы и будете правы, потому что последние окружности выходят за пределы экрана справа. Но с этой проблемой я предлагаю разобраться вам самостоятельно.
Потренируемся.
193. Напишите программу, изображающую "орбиты", соприкасающиеся все в крайней правой точке и имеющие разные радиусы (рис. 1.50).

Рис. 1.50. "Орбиты"
194. Создайте программу, выводящую на экран "труба" – окружности одного радиуса, выходящие из левого верхнего угла экрана и идущие под углом 45° вправо вниз (рис. 1.51). Окружности нарисованы одним цветом, а закрашены другим.
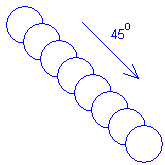
Рис. 1.51. "Труба" под углом 45°
