Вложенные циклы
А теперь два интегрированных задания, где надо применить знания, приобретенные вами ранее.
207. Напишите программу "Уничтожение астероида". Экран заполняется пятьюстами звездами. Астероид изображается красным кругом белым контуром, центром в точке 470, 160 и радиусом 10. По траектории функции y = 0.5sin2x + 2cos-x/2 от правой стороны экрана движется боевой звездолет, изображаемый зеленым кругом с желтым контуром и радиусом 3.
Каждый момент продвижения сопровождается проверкой условия, не находится ли звездолет в опасной близости от астероида (опасным считается расстояние менее 50 экранных точек). Если это расстояние в некоторый момент времени стало меньше критического, то звездолет уничтожает астероид, т. е. он взрывается (см. задание 179). На экране появляется торжествующая надпись. Все радуются (в том числе и учитель).
Совет
Расстояние между двумя точками на плоскости вычисляется по формуле: корень квадратный из суммы квадратов разностей координат Х1, Х2 и Y1, Y2. Я специально не пишу эту формулу. Проверяем понимание сложных инструкций.
208. Это задание носит прикладной характер и позволяет опытным путем вычислить число п. Да, безусловно, практически все из вас знают это число с точностью по крайней мере до двух знаков. Но предлагаемый метод очень хорош. Называется он методом Монте-Карло. Монте-Карло – европейская столица игорного бизнеса, а значит там владычествует Его Величество Случай. Вот "мы и попробуем поставить его себе на службу.
Сначала забудьте, чему равно п и послушайте теорию вопроса. Представьте себе окружность радиусом R = \, вписанную в квадрат. Из этого следует, что сторона квадрата будет 2R, а его площадь SK = (2R)2 =4R2. Площадь круга SO = kR2. Далее берем и равномерно посыпаем квадрат песком. Затем нанимаем бригаду рабочих, которые считают, сколько песчинок всего (N1) и сколько из них попало в круг (N2). Потом составляется простая пропорция – площадь квадрата так относится к площади круга, как общее количество песчинок к количеству песчинок попавших в круг.
Отсюда сенсационный вывод – радиус окружности не имеет никакого значения, она должна быть лишь вписана в квадрат (рис. 1.62).
Но где ж мы найдем песок, а главное тех, кто все это будет считать? Поэтому поставим компьютерный эксперимент. Нарисуем квадрат и впишем в него окружность. Координаты опорных точек (если сами рисовали) знаем. Уравнение окружности X2 +Y2 = R2 тоже знаем. Задаем цикл до 1000, в котором случайным образом определяем координаты "песчинок" так, чтобы они лежали внутри квадрата. Тут же проверяем условие, а не попала ли "песчинка" в круг (используя уравнение окружности), и если попала, подсчитываем их количество. Кроме того, рисуем их на экране разными цветами (попавшие и не попавшие).
По окончании цикла подсчитываем и выводим на экран число π. Понятно, что чем больше количество "песчинок", тем более точным будет результат. Для того чтобы знать, когда закончится эксперимент, рекомендуется выводить на экран счетчик "песчинок" (как мы делали с хронометром). Но, все-таки, экспериментировать с миллионом "песчинок" не надо – замучаетесь ждать сами, да и компьютер, хотя и железный, но все же живой.
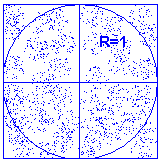
Рис. 1.62. Вычисление числа я методом Монте-Карло