Пример с матрицей
Напомним, что нашей задачей является найти значения температуры или любой другой функции U во всем множестве точек М = {1, 2,…, N-2, N-1}, считая, что в двух точках {О, N} она известна. Переход к конечным разностям производится с помощью трехточечного шаблона, который изображен на рис. 11.2.
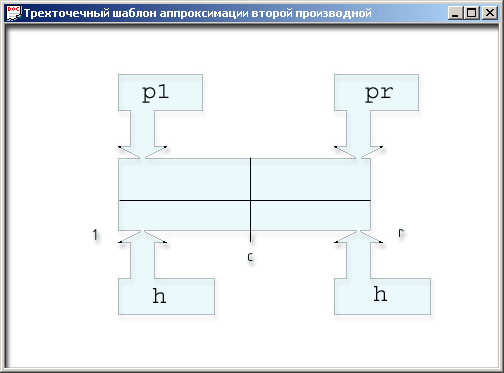
Рис. 11.2. Трехточечный шаблон аппроксимации второй производной
Мы имеем три точки и два отрезка, которых вполне достаточно, чтобы справиться со второй производной при попытке ее приближенного вычисления. Индексы I, r и с означают left, right и center. Обозначение pi принято для коэффициента, учитывающего свойства среды левого отрезка, например теплопроводности, а рг – правого. Шаги разбиения области вдоль оси х считаются одинаковыми и равными h. Теперь вы должны представить себе, что центр этого шаблона по очереди приставляется ко всем точкам из множества М. В результате этой процедуры мы по одному будем получать все |М| = N – 1 алгебраических уравнений, приближенно заменяющих одно дифференциальное уравнение Пуассона, которое, как говорят физики, удовлетворяется во всех точках этой части реального пространства.
Возвращаясь к шаблону из трех точек, напомним, что производная по х – это в некотором роде степень изменения функции, то есть скорость ее роста или падения вдоль этой координаты. Приближенно она равна:
dU/dx=(Ur-Uc)/h
Для правого отрезка и для левого:
dU/dx=(Uc-Ul)/h
Теперь надо записать приближенную оценку для второй производной с учетом коэффициента теплопроводности. Он может иметь разные значения (рI и рг) в левой и в правой частях шаблона:
d /dx(pdU/dx)={(pr[Ur-Uc])/h-(pl[Uc-Ul])/h }/h (2)
Произведя подстановку в исходное дифференциальное уравнение (1) и упростив выражение, получим алгебраическое уравнение:
aUl+bUc+cUr=0 (3)
