Алгоритмы упорядочения
Алгоритм упорядочения для симметрических матриц основан на алгоритме упорядочения по разреженности столбцов. Фактически symmmd(S) только формирует матрицу К с такой структурой ненулевых элементов, что К' *К имеет тот же трафик разреженности, что и S, и затем вызывает алгоритм упорядочения по разреженности столбцов для К. На рис. 12.2 приводится пример применения функции symmmd к элементам разреженной матрицы.
Пример:
>> B=bucky;p=symmmd(B); >> R=B(p,p); >> subplot(1.2.1),spy(B); subplot(1.2.2).spy(R);- r = symrcm(S) – возвращает вектор упорядоченности для симметричной матрицы S и называется упорядочением Катхилла-Макки. Причем формируется такая перестановка г, что S(r.r) будет концентрировать ненулевые элементы вблизи диагонали. Это хорошее упорядочение как перед LU-разложением, так и перед разложением Холецкого. Упорядочение применимо как для симметрических, так и для несимметрических матриц.
Для вещественной симметрической разреженной матрицы S (такой, что S=ST) собственные значения S(r.r) совпадают с собственными значениями S, но для вычисления eig(S(r,r)) требуется меньше времени, чем для вычисления eig(S).
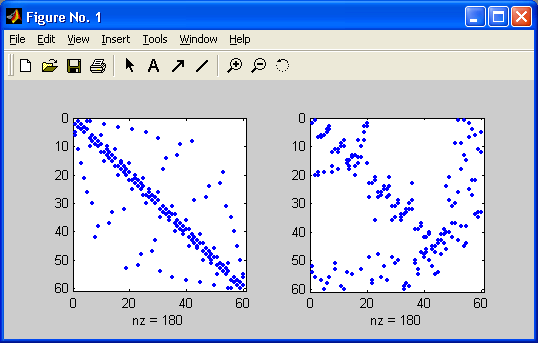
Рис. 12.2. Пример применения функции symmmd
Пример:
>> B=bucky;p=symrcm(B); >> R=B(p,p); >> subplot(1.2.1),spy(B);subplot(1.2.2),spy(R);На рис. 12.3 приведен пример концентрации ненулевых элементов разреженной матрицы вблизи главной диагонали.
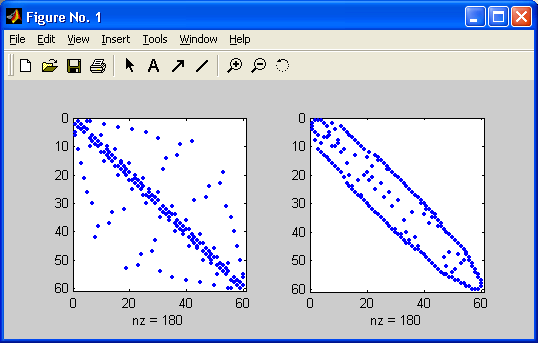
Рис. 12.3. Пример применения функции symrcm
