Отслеживание зависимостей. Релаксация в сети.
Строго говоря, термин "релаксация" относится к сети, а не к теории. Но сеть есть не что иное, как только представление определенной теории, например сеть а) является представлением теории:
f= mа т=3 а = 2,
В которой формула f= mа играет роль принудительного ограничения.
Сеть б) представляет теорию:
f = mа т=3 а = 2 f=6,
Которая находится в состоянии релаксации по отношению к ограничению f= та, а сеть в) представляет противоречивую теорию:
f = mа т=-3 а = 2 f =7.
По ходу изложения, не оговаривая отдельно, мы будем "перескакивать" от сетей к теориям, а для простоты использовать термин "представление", если нежелательно подчеркивать различие между этими двумя способами-реализации фактов и ограничений.
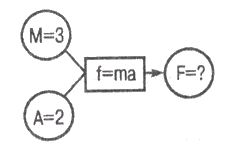
Рис. 19.1, a) Сети зависимостей с принудительными ограничениями. Окружностями представлены узлы сети, а прямоугольниками – связи
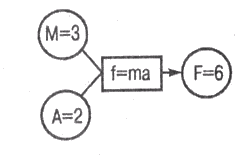
Рис. 19.1, б)
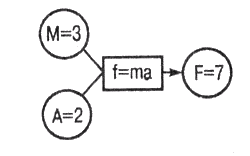
Рис. 19.1, в)
